LibFile: paths.scad
A path is a list of points of the same dimensions, usually 2D or 3D, that can
be connected together to form a sequence of line segments or a polygon.
A region is a list of paths that represent polygons, and the functions
in this file work on paths and also 1-regions, which are regions
that include exactly one path. When you pass a 1-region to a function, the default
value for closed is always true because regions represent polygons.
Capabilities include computing length of paths, computing
path tangents and normals, resampling of paths, and cutting paths up into smaller paths.
To use, add the following lines to the beginning of your file:
include <BOSL2/std.scad>
File Contents
-
is_path()– Returns True if 'list' is a path.is_1region()– Returns true if path is a region with one component.force_path()– Checks that path is a region with one component. [Path]path_merge_collinear()– Removes unnecessary points from a path. [Path]
-
Section: Path length calculation
path_length()– Returns the path length.path_segment_lengths()– Returns a list of the lengths of segments in a path.path_length_fractions()– Returns the fractional distance of each point along the length of a path.
-
Section: Resampling - changing the number of points in a path
subdivide_path()– Subdivides a path to produce a more finely sampled path. [Path]resample_path()– Returns an equidistant set of points along a path. [Path]
-
is_path_simple()– Returns true if a path has no self intersections.path_closest_point()– Returns the closest place on a path to a given point.path_tangents()– Returns tangent vectors for each point along a path.path_normals()– Returns normal vectors for each point along a path.path_curvature()– Returns the estimated numerical curvature of the path.path_torsion()– Returns the estimated numerical torsion of the path.
-
Section: Breaking paths up into subpaths
path_cut()– Cuts a path into subpaths at various points. [PathList]path_cut_points()– Returns a list of cut points at a list of distances from the first point in a path.split_path_at_self_crossings()– Split a 2D path wherever it crosses itself. [PathList]polygon_parts()– Parses a self-intersecting polygon into a list of non-intersecting polygons. [PathList]
Section: Utility Functions
Function: is_path()
Synopsis: Returns True if 'list' is a path.
Topics: Paths
See Also: is_region(), is_vnf()
Usage:
- is_path(list, [dim], [fast])
Description:
Returns true if list is a path. A path is a list of two or more numeric vectors (AKA points).
All vectors must of the same size, and may only contain numbers that are not inf or nan.
By default the vectors in a path must be 2d or 3d. Set the dim parameter to specify a list
of allowed dimensions, or set it to undef to allow any dimension. (Note that this function
returns false on 1-regions.)
Arguments:
| By Position | What it does |
|---|---|
list |
list to check |
dim |
list of allowed dimensions of the vectors in the path. Default: [2,3] |
fast |
set to true for fast check that only looks at first entry. Default: false |
Example 1:
include <BOSL2/std.scad>
bool1 = is_path([[3,4],[5,6]]); // Returns true
bool2 = is_path([[3,4]]); // Returns false
bool3 = is_path([[3,4],[4,5]],2); // Returns true
bool4 = is_path([[3,4,3],[5,4,5]],2); // Returns false
bool5 = is_path([[3,4,3],[5,4,5]],2); // Returns false
bool6 = is_path([[3,4,5],undef,[4,5,6]]); // Returns false
bool7 = is_path([[3,5],[undef,undef],[4,5]]); // Returns false
bool8 = is_path([[3,4],[5,6],[5,3]]); // Returns true
bool9 = is_path([3,4,5,6,7,8]); // Returns false
bool10 = is_path([[3,4],[5,6]], dim=[2,3]);// Returns true
bool11 = is_path([[3,4],[5,6]], dim=[1,3]);// Returns false
bool12 = is_path([[3,4],"hello"], fast=true); // Returns true
bool13 = is_path([[3,4],[3,4,5]]); // Returns false
bool14 = is_path([[1,2,3,4],[2,3,4,5]]); // Returns false
bool15 = is_path([[1,2,3,4],[2,3,4,5]],undef);// Returns true
Function: is_1region()
Synopsis: Returns true if path is a region with one component.
See Also: force_path()
Usage:
- bool = is_1region(path, [name])
Description:
If path is a region with one component (a 1-region) then return true. If path is a region with more components
then display an error message about the parameter name requiring a path or a single component region. If the input
is not a region then return false. This function helps path functions accept 1-regions.
Arguments:
| By Position | What it does |
|---|---|
path |
input to process |
name |
name of parameter to use in error message. Default: "path" |
Function: force_path()
Synopsis: Checks that path is a region with one component. [Path]
See Also: is_1region()
Usage:
- outpath = force_path(path, [name])
Description:
If path is a region with one component (a 1-region) then returns that component as a path.
If path is a region with more components then displays an error message about the parameter
name requiring a path or a single component region. If the input is not a region then
returns the input without any checks. This function helps path functions accept 1-regions.
Arguments:
| By Position | What it does |
|---|---|
path |
input to process |
name |
name of parameter to use in error message. Default: "path" |
Function: path_merge_collinear()
Synopsis: Removes unnecessary points from a path. [Path]
Usage:
- path_merge_collinear(path, [eps])
Description:
Takes a path and removes unnecessary sequential collinear points. Note that when closed=true either of the path
endpoints may be removed.
Arguments:
| By Position | What it does |
|---|---|
path |
A path of any dimension or a 1-region |
closed |
treat as closed polygon. Default: false |
eps |
Largest positional variance allowed. Default: EPSILON (1-e9) |
Section: Path length calculation
Function: path_length()
Synopsis: Returns the path length.
Topics: Paths
See Also: path_segment_lengths(), path_length_fractions()
Usage:
- path_length(path,[closed])
Description:
Returns the length of the path.
Arguments:
| By Position | What it does |
|---|---|
path |
Path of any dimension or 1-region. |
closed |
true if the path is closed. Default: false |
Example 1:
include <BOSL2/std.scad>
path = [[0,0], [5,35], [60,-25], [80,0]];
echo(path_length(path));
Function: path_segment_lengths()
Synopsis: Returns a list of the lengths of segments in a path.
Topics: Paths
See Also: path_length(), path_length_fractions()
Usage:
- path_segment_lengths(path,[closed])
Description:
Returns list of the length of each segment in a path
Arguments:
| By Position | What it does |
|---|---|
path |
path in any dimension or 1-region |
closed |
true if the path is closed. Default: false |
Function: path_length_fractions()
Synopsis: Returns the fractional distance of each point along the length of a path.
Topics: Paths
See Also: path_length(), path_segment_lengths()
Usage:
- fracs = path_length_fractions(path, [closed]);
Description:
Returns the distance fraction of each point in the path along the path, so the first point is zero and the final point is 1. If the path is closed the length of the output will have one extra point because of the final connecting segment that connects the last point of the path to the first point.
Arguments:
| By Position | What it does |
|---|---|
path |
path in any dimension or a 1-region |
closed |
set to true if path is closed. Default: false |
Section: Resampling - changing the number of points in a path
Function: subdivide_path()
Synopsis: Subdivides a path to produce a more finely sampled path. [Path]
Topics: Paths, Path Subdivision
See Also: subdivide_and_slice(), resample_path(), jittered_poly()
Usage:
- newpath = subdivide_path(path, n|refine=|maxlen=, [method=], [closed=], [exact=]);
Description:
Takes a path as input (closed or open) and subdivides the path to produce a more
finely sampled path. You control the subdivision process by using the maxlen arg
to specify a maximum segment length, or by specifying n or refine, which request
a certain point count in the output.
You can specify the point count using the n option, where
you give the number of points you want in the output, or you can use
the refine option, where you specify a resampling factor. If refine=3 then
the number of points would increase by a factor of three, so a four point square would
have 12 points after subdivision. With point-count subdivision, the new points can be distributed
proportional to length (method="length"), which is the default, or they can be divided up evenly among all the path segments
(method="segment"). If the extra points don't fit evenly on the path then the
algorithm attempts to distribute them as uniformly as possible, but the result may be uneven.
The exact option, which is true by default, requires that the final point count is
exactly as requested. For example, if you subdivide a four point square and request n=13 then one edge will have
an extra point compared to the others.
If you set exact=false then the
algorithm will favor uniformity and the output path may have a different number of
points than you requested, but the sampling will be uniform. In our example of the
square with n=13, you will get only 12 points output, with the same number of points on each edge.
The points are always distributed uniformly on each segment. The method="length" option does
means that the number of points on a segment is based on its length, but the points are still
distributed uniformly on each segment, independent of the other segments.
With the "segment" method you can also give n as a vector of counts. This
specifies the desired point count on each segment: with vector valued n the subdivide_path
function places n[i]-1 points on segment i. The reason for the -1 is to avoid
double counting the endpoints, which are shared by pairs of segments, so that for
a closed polygon the total number of points will be sum(n). Note that with an open
path there is an extra point at the end, so the number of points will be sum(n)+1.
If you use the maxlen option then you specify the maximum length segment allowed in the output.
Each segment is subdivided into the largest number of segments meeting your requirement. As above,
the sampling is uniform on each segment, independent of the other segments. With the maxlen option
you cannot specify method or exact.
Arguments:
| By Position | What it does |
|---|---|
path |
path in any dimension or a 1-region |
n |
scalar total number of points desired or with method="segment" can be a vector requesting n[i]-1 new points added to segment i. |
| By Name | What it does |
|---|---|
refine |
increase total number of points by this factor (Specify only one of n, refine and maxlen) |
maxlen |
maximum length segment in the output (Specify only one of n, refine and maxlen) |
closed |
set to false if the path is open. Default: True |
exact |
if true return exactly the requested number of points, possibly sacrificing uniformity. If false, return uniform point sample that may not match the number of points requested. (Not allowed with maxlen.) Default: true |
method |
One of "length" or "segment". If "length", adds vertices in proportion to segment length, so short segments get fewer points. If "segment", add points evenly among the segments, so all segments get the same number of points. (Not allowed with maxlen.) Default: "length" |
Example 1:
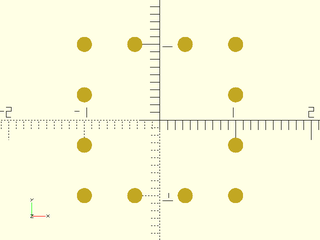
include <BOSL2/std.scad>
mypath = subdivide_path(square([2,2],center=true), 12);
move_copies(mypath)circle(r=.1,$fn=32);
Example 2:
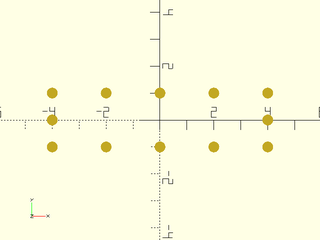
include <BOSL2/std.scad>
mypath = subdivide_path(square([8,2],center=true), 12);
move_copies(mypath)circle(r=.2,$fn=32);
Example 3:
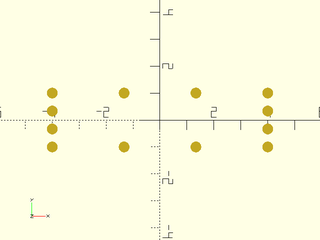
include <BOSL2/std.scad>
mypath = subdivide_path(square([8,2],center=true), 12, method="segment");
move_copies(mypath)circle(r=.2,$fn=32);
Example 4:
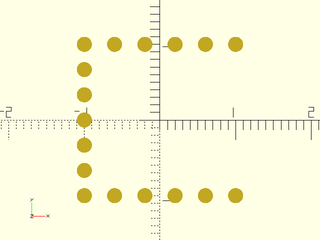
include <BOSL2/std.scad>
mypath = subdivide_path(square([2,2],center=true), 17, closed=false);
move_copies(mypath)circle(r=.1,$fn=32);
Example 5: Specifying different numbers of points on each segment
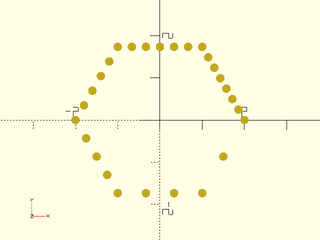
include <BOSL2/std.scad>
mypath = subdivide_path(hexagon(side=2), [2,3,4,5,6,7], method="segment");
move_copies(mypath)circle(r=.1,$fn=32);
Example 6: Requested point total is 14 but 15 points output due to extra end point
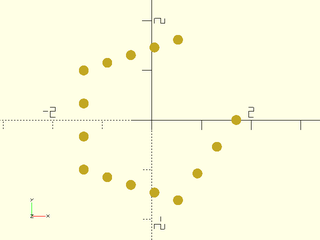
include <BOSL2/std.scad>
mypath = subdivide_path(pentagon(side=2), [3,4,3,4], method="segment", closed=false);
move_copies(mypath)circle(r=.1,$fn=32);
Example 7: Since 17 is not divisible by 5, a completely uniform distribution is not possible.
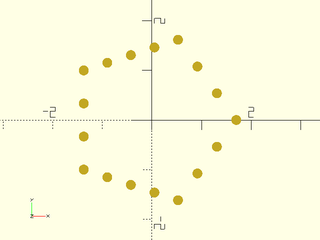
include <BOSL2/std.scad>
mypath = subdivide_path(pentagon(side=2), 17);
move_copies(mypath)circle(r=.1,$fn=32);
Example 8: With exact=false a uniform distribution, but only 15 points
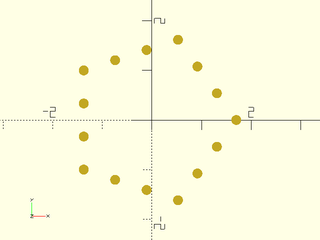
include <BOSL2/std.scad>
mypath = subdivide_path(pentagon(side=2), 17, exact=false);
move_copies(mypath)circle(r=.1,$fn=32);
Example 9: With exact=false you can also get extra points, here 20 instead of requested 18
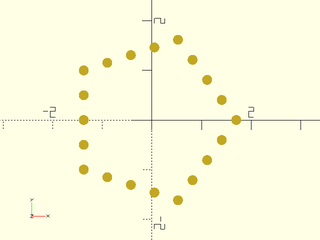
include <BOSL2/std.scad>
mypath = subdivide_path(pentagon(side=2), 18, exact=false);
move_copies(mypath)circle(r=.1,$fn=32);
Example 10: Using refine in this example multiplies the point count by 3 by adding 2 points to each edge
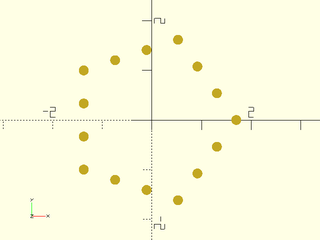
include <BOSL2/std.scad>
mypath = subdivide_path(pentagon(side=2), refine=3);
move_copies(mypath)circle(r=.1,$fn=32);
Example 11: But note that refine doesn't distribute evenly by segment unless you change the method. with the default method set to "length", the points are distributed with more on the long segments in this example using refine.
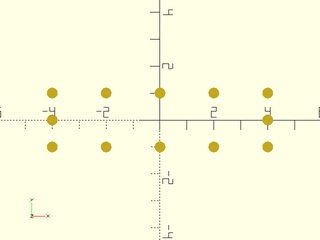
include <BOSL2/std.scad>
mypath = subdivide_path(square([8,2],center=true), refine=3);
move_copies(mypath)circle(r=.2,$fn=32);
Example 12: In this example with maxlen, every side gets a different number of new points
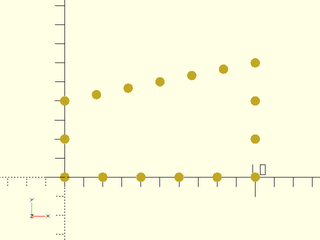
include <BOSL2/std.scad>
path = [[0,0],[0,4],[10,6],[10,0]];
spath = subdivide_path(path, maxlen=2, closed=true);
move_copies(spath) circle(r=.25,$fn=12);
Example 13: Three-dimensional paths also work
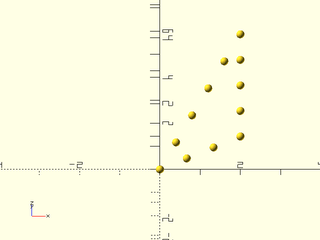
include <BOSL2/std.scad>
mypath = subdivide_path([[0,0,0],[2,0,1],[2,3,2]], 12);
move_copies(mypath)sphere(r=.1,$fn=32);
Function: resample_path()
Synopsis: Returns an equidistant set of points along a path. [Path]
Topics: Paths
See Also: subdivide_path()
Usage:
- newpath = resample_path(path, n|spacing=, [closed=]);
Description:
Compute a uniform resampling of the input path. If you specify n then the output path will have n
points spaced uniformly (by linear interpolation along the input path segments). The only points of the
input path that are guaranteed to appear in the output path are the starting and ending points, and any
points that have an angular deflection of at least the number of degrees given in keep_corners.
If you specify spacing then the length you give will be rounded to the nearest spacing that gives
a uniform sampling of the path and the resulting uniformly sampled path is returned.
Note that because this function operates on a discrete input path the quality of the output depends on
the sampling of the input. If you want very accurate output, use a lot of points for the input.
Arguments:
| By Position | What it does |
|---|---|
path |
path in any dimension or a 1-region |
n |
Number of points in output |
| By Name | What it does |
|---|---|
spacing |
Approximate spacing desired |
keep_corners |
If given a scalar, path vertices with deflection angle greater than this are preserved in the output. |
closed |
set to true if path is closed. Default: true |
Example 1: Subsampling lots of points from a smooth curve
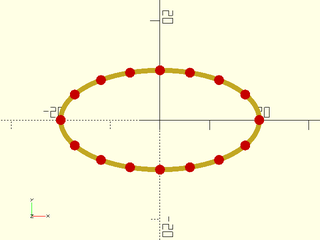
include <BOSL2/std.scad>
path = xscale(2,circle($fn=250, r=10));
sampled = resample_path(path, 16);
stroke(path);
color("red")move_copies(sampled) circle($fn=16);
Example 2: Specified spacing is rounded to make a uniform sampling
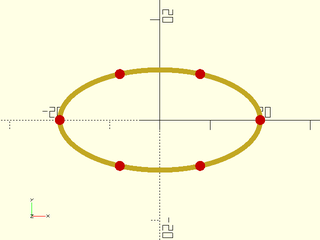
include <BOSL2/std.scad>
path = xscale(2,circle($fn=250, r=10));
sampled = resample_path(path, spacing=17);
stroke(path);
color("red")move_copies(sampled) circle($fn=16);
Example 3: Notice that the corners are excluded.
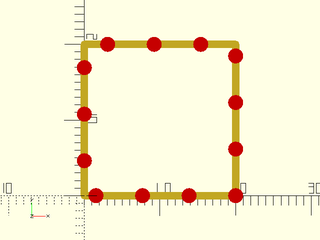
include <BOSL2/std.scad>
path = square(20);
sampled = resample_path(path, spacing=6);
stroke(path,closed=true);
color("red")move_copies(sampled) circle($fn=16);
Example 4: Forcing preservation of corners.
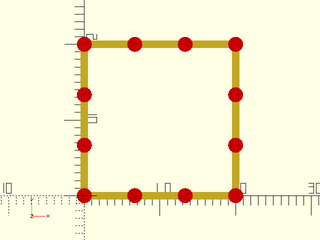
include <BOSL2/std.scad>
path = square(20);
sampled = resample_path(path, spacing=6, keep_corners=90);
stroke(path,closed=true);
color("red")move_copies(sampled) circle($fn=16);
Example 5: Closed set to false
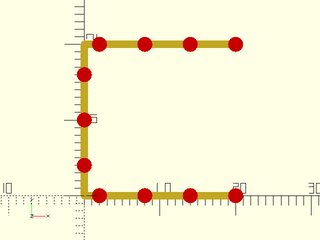
include <BOSL2/std.scad>
path = square(20);
sampled = resample_path(path, spacing=6,closed=false);
stroke(path);
color("red")move_copies(sampled) circle($fn=16);
Section: Path Geometry
Function: is_path_simple()
Synopsis: Returns true if a path has no self intersections.
Topics: Paths
See Also: is_path()
Usage:
- bool = is_path_simple(path, [closed], [eps]);
Description:
Returns true if the given 2D path is simple, meaning that it has no self-intersections. Repeated points are not considered self-intersections: a path with such points can still be simple. If closed is set to true then treat the path as a polygon.
Arguments:
| By Position | What it does |
|---|---|
path |
2D path or 1-region |
closed |
set to true to treat path as a polygon. Default: false |
eps |
Epsilon error value used for determine if points coincide. Default: EPSILON (1e-9) |
Function: path_closest_point()
Synopsis: Returns the closest place on a path to a given point.
Topics: Paths
See Also: point_line_distance(), line_closest_point()
Usage:
- index_pt = path_closest_point(path, pt);
Description:
Finds the closest path segment, and point on that segment to the given point.
Returns [SEGNUM, POINT]
Arguments:
| By Position | What it does |
|---|---|
path |
Path of any dimension or a 1-region. |
pt |
The point to find the closest point to. |
closed |
If true, the path is considered closed. |
Example 1:
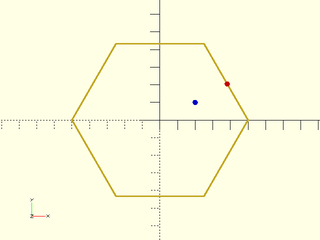
include <BOSL2/std.scad>
path = circle(d=100,$fn=6);
pt = [20,10];
closest = path_closest_point(path, pt);
stroke(path, closed=true);
color("blue") translate(pt) circle(d=3, $fn=12);
color("red") translate(closest[1]) circle(d=3, $fn=12);
Function: path_tangents()
Synopsis: Returns tangent vectors for each point along a path.
Topics: Paths
See Also: path_normals()
Usage:
- tangs = path_tangents(path, [closed], [uniform]);
Description:
Compute the tangent vector to the input path. The derivative approximation is described in deriv().
The returns vectors will be normalized to length 1. If any derivatives are zero then
the function fails with an error. If you set uniform to false then the sampling is
assumed to be non-uniform and the derivative is computed with adjustments to produce corrected
values.
Arguments:
| By Position | What it does |
|---|---|
path |
path of any dimension or a 1-region |
closed |
set to true of the path is closed. Default: false |
uniform |
set to false to correct for non-uniform sampling. Default: true |
Example 1: A shape with non-uniform sampling gives distorted derivatives that may be undesirable. Note that derivatives tilt towards the long edges of the rectangle.
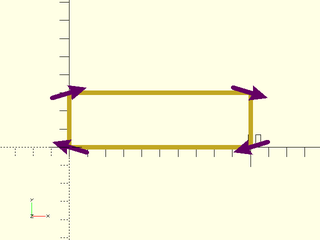
include <BOSL2/std.scad>
rect = square([10,3]);
tangents = path_tangents(rect,closed=true);
stroke(rect,closed=true, width=0.25);
color("purple")
for(i=[0:len(tangents)-1])
stroke([rect[i]-tangents[i], rect[i]+tangents[i]],width=.25, endcap2="arrow2");
Example 2: Setting uniform to false corrects the distorted derivatives for this example:
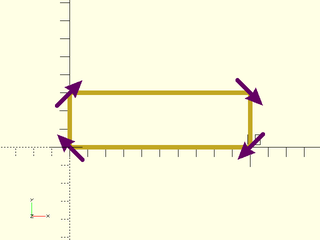
include <BOSL2/std.scad>
rect = square([10,3]);
tangents = path_tangents(rect,closed=true,uniform=false);
stroke(rect,closed=true, width=0.25);
color("purple")
for(i=[0:len(tangents)-1])
stroke([rect[i]-tangents[i], rect[i]+tangents[i]],width=.25, endcap2="arrow2");
Function: path_normals()
Synopsis: Returns normal vectors for each point along a path.
Topics: Paths
See Also: path_tangents()
Usage:
- norms = path_normals(path, [tangents], [closed]);
Description:
Compute the normal vector to the input path. This vector is perpendicular to the path tangent and lies in the plane of the curve. For 3d paths we define the plane of the curve at path point i to be the plane defined by point i and its two neighbors. At the endpoints of open paths we use the three end points. For 3d paths the computed normal is the one lying in this plane that points towards the center of curvature at that path point. For 2d paths, which lie in the xy plane, the normal is the path pointing to the right of the direction the path is traveling. If points are collinear then a 3d path has no center of curvature, and hence the normal is not uniquely defined. In this case the function issues an error. For 2d paths the plane is always defined so the normal fails to exist only when the derivative is zero (in the case of repeated points).
Arguments:
| By Position | What it does |
|---|---|
path |
2D or 3D path or a 1-region |
tangents |
path tangents optionally supplied |
closed |
if true path is treated as a polygon. Default: false |
Function: path_curvature()
Synopsis: Returns the estimated numerical curvature of the path.
Topics: Paths
See Also: path_tangents(), path_normals(), path_torsion()
Usage:
- curvs = path_curvature(path, [closed]);
Description:
Numerically estimate the curvature of the path (in any dimension).
Arguments:
| By Position | What it does |
|---|---|
path |
path in any dimension or a 1-region |
closed |
if true then treat the path as a polygon. Default: false |
Function: path_torsion()
Synopsis: Returns the estimated numerical torsion of the path.
Topics: Paths
See Also: path_tangents(), path_normals(), path_curvature()
Usage:
- torsions = path_torsion(path, [closed]);
Description:
Numerically estimate the torsion of a 3d path.
Arguments:
| By Position | What it does |
|---|---|
path |
3D path |
closed |
if true then treat path as a polygon. Default: false |
Section: Breaking paths up into subpaths
Function: path_cut()
Synopsis: Cuts a path into subpaths at various points. [PathList]
Topics: Paths, Path Subdivision
See Also: split_path_at_self_crossings(), path_cut_points()
Usage:
- path_list = path_cut(path, cutdist, [closed]);
Description:
Given a list of distances in cutdist, cut the path into
subpaths at those lengths, returning a list of paths.
If the input path is closed then the final path will include the
original starting point. The list of cut distances must be
in ascending order and should not include the endpoints: 0
or len(path). If you repeat a distance you will get an
empty list in that position in the output. If you give an
empty cutdist array you will get the input path as output
(without the final vertex doubled in the case of a closed path).
Arguments:
| By Position | What it does |
|---|---|
path |
path of any dimension or a 1-region |
cutdist |
Distance or list of distances where path is cut |
closed |
If true, treat the path as a closed polygon. Default: false |
Example 1:
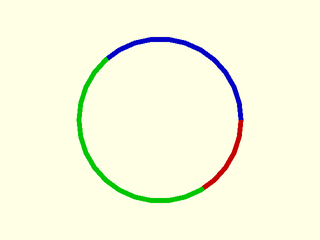
include <BOSL2/std.scad>
path = circle(d=100);
segs = path_cut(path, [50, 200], closed=true);
rainbow(segs) stroke($item, endcaps="butt", width=3);
Function: path_cut_points()
Synopsis: Returns a list of cut points at a list of distances from the first point in a path.
Topics: Paths, Path Subdivision
See Also: path_cut(), split_path_at_self_crossings()
Usage:
- cuts = path_cut_points(path, cutdist, [closed=], [direction=]);
Description:
Cuts a path at a list of distances from the first point in the path. Returns a list of the cut
points and indices of the next point in the path after that point. So for example, a return
value entry of [[2,3], 5] means that the cut point was [2,3] and the next point on the path after
this point is path[5]. If the path is too short then path_cut_points returns undef. If you set
direction to true then path_cut_points will also return the tangent vector to the path and a normal
vector to the path. It tries to find a normal vector that is coplanar to the path near the cut
point. If this fails it will return a normal vector parallel to the xy plane. The output with
direction vectors will be [point, next_index, tangent, normal].
If you give the very last point of the path as a cut point then the returned index will be one larger than the last index (so it will not be a valid index). If you use the closed option then the returned index will be equal to the path length for cuts along the closing path segment, and if you give a point equal to the path length you will get an index of len(path)+1 for the index.
Arguments:
| By Position | What it does |
|---|---|
path |
path to cut |
cutdist |
distances where the path should be cut (a list) or a scalar single distance |
| By Name | What it does |
|---|---|
closed |
set to true if the curve is closed. Default: false |
direction |
set to true to return direction vectors. Default: false |
Example 1:
include <BOSL2/std.scad>
square=[[0,0],[1,0],[1,1],[0,1]];
path_cut_points(square, [.5,1.5,2.5]); // Returns [[[0.5, 0], 1], [[1, 0.5], 2], [[0.5, 1], 3]]
path_cut_points(square, [0,1,2,3]); // Returns [[[0, 0], 1], [[1, 0], 2], [[1, 1], 3], [[0, 1], 4]]
path_cut_points(square, [0,0.8,1.6,2.4,3.2], closed=true); // Returns [[[0, 0], 1], [[0.8, 0], 1], [[1, 0.6], 2], [[0.6, 1], 3], [[0, 0.8], 4]]
path_cut_points(square, [0,0.8,1.6,2.4,3.2]); // Returns [[[0, 0], 1], [[0.8, 0], 1], [[1, 0.6], 2], [[0.6, 1], 3], undef]
Function: split_path_at_self_crossings()
Synopsis: Split a 2D path wherever it crosses itself. [PathList]
Topics: Paths, Path Subdivision
See Also: path_cut(), path_cut_points()
Usage:
- paths = split_path_at_self_crossings(path, [closed], [eps]);
Description:
Splits a 2D path into sub-paths wherever the original path crosses itself. Splits may occur mid-segment, so new vertices will be created at the intersection points. Returns a list of the resulting subpaths.
Arguments:
| By Position | What it does |
|---|---|
path |
A 2D path or a 1-region. |
closed |
If true, treat path as a closed polygon. Default: true |
eps |
Acceptable variance. Default: EPSILON (1e-9) |
Example 1:
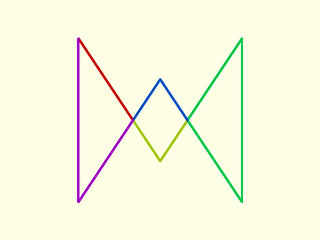
include <BOSL2/std.scad>
path = [ [-100,100], [0,-50], [100,100], [100,-100], [0,50], [-100,-100] ];
paths = split_path_at_self_crossings(path);
rainbow(paths) stroke($item, closed=false, width=3);
Function: polygon_parts()
Synopsis: Parses a self-intersecting polygon into a list of non-intersecting polygons. [PathList]
See Also: split_path_at_self_crossings(), path_cut(), path_cut_points()
Usage:
- splitpolys = polygon_parts(poly, [nonzero], [eps]);
Description:
Given a possibly self-intersecting 2d polygon, constructs a representation of the original polygon as a list of non-intersecting simple polygons. If nonzero is set to true then it uses the nonzero method for defining polygon membership. For simple cases, such as the pentagram, this will produce the outer perimeter of a self-intersecting polygon.
Arguments:
| By Position | What it does |
|---|---|
poly |
a 2D polygon or 1-region |
nonzero |
If true use the nonzero method for checking if a point is in a polygon. Otherwise use the even-odd method. Default: false |
eps |
The epsilon error value to determine whether two points coincide. Default: EPSILON (1e-9) |
Example 1: This cross-crossing polygon breaks up into its 3 components (regardless of the value of nonzero).
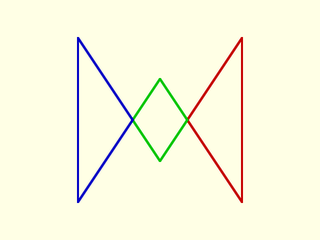
include <BOSL2/std.scad>
poly = [
[-100,100], [0,-50], [100,100],
[100,-100], [0,50], [-100,-100]
];
splitpolys = polygon_parts(poly);
rainbow(splitpolys) stroke($item, closed=true, width=3);
Example 2: With nonzero=false you get even-odd mode which matches OpenSCAD, so the pentagram breaks apart into its five points.
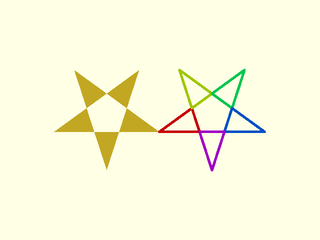
include <BOSL2/std.scad>
pentagram = turtle(["move",100,"left",144], repeat=4);
left(100)polygon(pentagram);
rainbow(polygon_parts(pentagram,nonzero=false))
stroke($item,closed=true,width=2.5);
Example 3: With nonzero=true you get only the outer perimeter. You can use this to create the polygon using the nonzero method, which is not supported by OpenSCAD.
include <BOSL2/std.scad>
pentagram = turtle(["move",100,"left",144], repeat=4);
outside = polygon_parts(pentagram,nonzero=true);
left(100)region(outside);
rainbow(outside)
stroke($item,closed=true,width=2.5);
Example 4:
include <BOSL2/std.scad>
N=12;
ang=360/N;
sr=10;
poly = turtle(["angle", 90+ang/2,
"move", sr, "left",
"move", 2*sr*sin(ang/2), "left",
"repeat", 4,
["move", 2*sr, "left",
"move", 2*sr*sin(ang/2), "left"],
"move", sr]);
stroke(poly, width=.3);
right(20)rainbow(polygon_parts(poly)) polygon($item);
Example 5: overlapping poly segments disappear
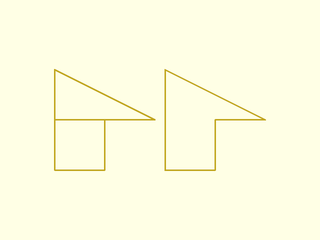
include <BOSL2/std.scad>
poly = [[0,0], [10,0], [10,10], [0,10],[0,20], [20,10],[10,10], [0,10],[0,0]];
stroke(poly,width=0.3);
right(22)stroke(polygon_parts(poly)[0], width=0.3, closed=true);
Example 6: Poly segments disappear outside as well
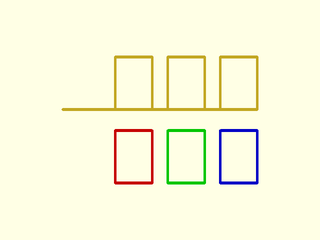
include <BOSL2/std.scad>
poly = turtle(["repeat", 3, ["move", 17, "left", "move", 10, "left", "move", 7, "left", "move", 10, "left"]]);
back(2)stroke(poly,width=.5);
fwd(12)rainbow(polygon_parts(poly)) stroke($item, closed=true, width=0.5);
Example 7: This shape has six components
include <BOSL2/std.scad>
poly = turtle(["repeat", 3, ["move", 15, "left", "move", 7, "left", "move", 10, "left", "move", 17, "left"]]);
polygon(poly);
right(22)rainbow(polygon_parts(poly)) polygon($item);
Example 8: When the loops of the shape overlap then nonzero gives a different result than the even-odd method.
include <BOSL2/std.scad>
poly = turtle(["repeat", 3, ["move", 15, "left", "move", 7, "left", "move", 10, "left", "move", 10, "left"]]);
polygon(poly);
right(27)rainbow(polygon_parts(poly)) polygon($item);
move([16,-14])rainbow(polygon_parts(poly,nonzero=true)) polygon($item);