LibFile: vnf.scad
The Vertices'N'Faces structure (VNF) holds the data used by polyhedron() to construct objects: a vertex list and a list of faces. This library makes it easier to construct polyhedra by providing functions to construct, merge, and modify VNF data, while avoiding common pitfalls such as reversed faces. It can find faults in your polyhedrons. Note that this file is for low level manipulation of lists of vertices and faces: it can perform some simple transformations on VNF structures but cannot perform boolean operations on the polyhedrons represented by VNFs.
To use, add the following lines to the beginning of your file:
include <BOSL2/std.scad>
File Contents
-
Section: Creating Polyhedrons with VNF Structures
vnf_vertex_array()– Returns a VNF structure from a rectangular vertex list. [VNF]vnf_tri_array()– Returns a VNF from an array of points. The array need not be rectangular. [VNF]vnf_join()– Returns a single VNF structure from a list of VNF structures. [VNF]vnf_from_polygons()– Returns a VNF from a list of 3D polygons. [VNF]vnf_from_region()– Returns a 3D VNF given a 2D region. [VNF]
-
Section: VNF Testing and Access
is_vnf()– Returns true given a VNF-like structure.is_vnf_list()– Returns true given a list of VNF-like structures.vnf_vertices()– Returns the list of vertex points from a VNF.vnf_faces()– Returns the list of faces from a VNF.
-
Section: Altering the VNF Internals
vnf_reverse_faces()– Reverses the faces of a VNF. [VNF]vnf_quantize()– Quantizes the vertex coordinates of a VNF. [VNF]vnf_merge_points()– Consolidates duplicate vertices of a VNF. [VNF]vnf_drop_unused_points()– Removes unreferenced vertices from a VNF. [VNF]vnf_triangulate()– Triangulates the faces of a VNF. [VNF]vnf_unify_faces()– Remove triangulation from VNF, returning a copy with full faces [VNF]vnf_slice()– Slice the faces of a VNF along an axis. [VNF]
-
Section: Turning a VNF into geometry
vnf_polyhedron()– Returns a polyhedron from a VNF or list of VNFs. [Geom]vnf_wireframe()– Creates a wireframe model from a VNF. [VNF]
-
vnf_volume()– Returns the volume of a VNF.vnf_area()– Returns the surface area of a VNF.projection()– Returns projection or intersection of vnf with XY plane [VNF]vnf_halfspace()– Returns the intersection of the vnf with a half space. [VNF]vnf_bend()– Bends a VNF around an axis. [VNF]vnf_hull()– Compute convex hull of VNF or 3d pathvnf_boundary()– Returns the boundary of a VNF as an list of paths [VNF]vnf_small_offset()– Computes an offset surface to a VNF for small offset distances [VNF]vnf_sheet()– Extends a VNF into a thin sheet by extruding normal to the VNF [VNF]
-
Section: Debugging Polyhedrons
debug_vnf()– A replacement forvnf_polyhedron()to help with debugging. [VNF]vnf_validate()– Echos non-manifold VNF errors to the console. [VNF]
Section: Creating Polyhedrons with VNF Structures
VNF stands for "Vertices'N'Faces". VNF structures are 2-item lists, [VERTICES,FACES] where the
first item is a list of vertex points, and the second is a list of face indices into the vertex
list. Each VNF is self contained, with face indices referring only to its own vertex list.
You can construct a polyhedron() in parts by describing each part in a self-contained VNF, then
merge the various VNFs to get the completed polyhedron vertex list and faces.
Function: vnf_vertex_array()
Synopsis: Returns a VNF structure from a rectangular vertex list. [VNF]
Topics: VNF Generators, Lists
See Also: vnf_tri_array(), vnf_join(), vnf_from_polygons(), vnf_from_region()
Usage:
- vnf = vnf_vertex_array(points, [caps=], [cap1=], [cap2=], [style=], [reverse=], [col_wrap=], [row_wrap=], [triangulate=]);
Description:
Creates a VNF structure from a rectangular vertex list, creating edges that connect the adjacent vertices in the vertex list and creating the faces defined by those edges. You can optionally create the edges and faces to wrap the last column back to the first column, or wrap the last row to the first. Endcaps can be added to either the first and/or last rows. The style parameter determines how the quadrilaterals are divided into triangles. The default style is an arbitrary, systematic subdivision in the same direction. The "alt" style is the uniform subdivision in the other (alternate) direction. The "flip1" style is an arbitrary division which alternates the direction for any adjacent pair of quadrilaterals. The "flip2" style is the alternating division that is the opposite of "flip1". The "min_edge" style picks the shorter edge to subdivide for each quadrilateral, so the division may not be uniform across the shape. The "quincunx" style adds a vertex in the center of each quadrilateral and creates four triangles, and the "convex" and "concave" styles choose the locally convex/concave subdivision. The "min_area" option creates the triangulation with the minimal area. Degenerate faces are not included in the output, but if this results in unused vertices they will still appear in the output.
Arguments:
| By Position | What it does |
|---|---|
points |
A list of vertices to divide into columns and rows. |
| By Name | What it does |
|---|---|
caps |
If true, add endcap faces to the first and last rows. |
cap1 |
If true, add an endcap face to the first row. |
cap2 |
If true, add an endcap face to the last row. |
col_wrap |
If true, add faces to connect the last column to the first. |
row_wrap |
If true, add faces to connect the last row to the first. |
reverse |
If true, reverse all face normals. |
style |
The style of subdividing the quads into faces. Valid options are "default", "alt", "flip1", "flip2", "min_edge", "min_area", "quincunx", "convex" and "concave". |
triangulate |
If true, triangulates endcaps to resolve possible CGAL issues. This can be an expensive operation if the endcaps are complex. Default: false |
Example 1:
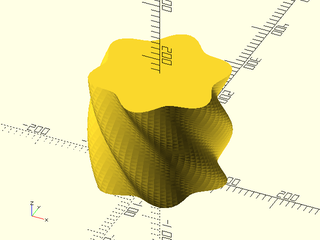
include <BOSL2/std.scad>
vnf = vnf_vertex_array(
points=[
for (h = [0:5:180-EPSILON]) [
for (t = [0:5:360-EPSILON])
cylindrical_to_xyz(100 + 12 * cos((h/2 + t)*6), t, h)
]
],
col_wrap=true, caps=true, reverse=true, style="alt"
);
vnf_polyhedron(vnf);
Example 2: Open shape made from a three arcs.
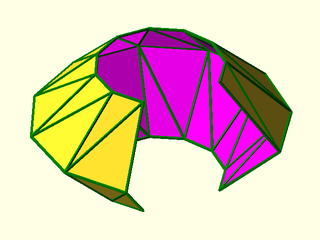
include <BOSL2/std.scad>
rows = [
for(h=[-20:20:20])
path3d(arc(r=40-abs(h), angle=280, 10), h)
];
vnf = vnf_vertex_array(rows, reverse=true);
vnf_polyhedron(vnf);
color("green") vnf_wireframe(vnf);
Example 3: Open shape made from a three arcs, with row_wrap=true.
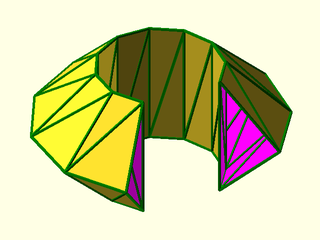
include <BOSL2/std.scad>
rows = [
for(h=[-20:20:20])
path3d(arc(r=40-abs(h), angle=280, 10), h)
];
vnf = vnf_vertex_array(rows, reverse=true, row_wrap=true);
vnf_polyhedron(vnf);
color("green") vnf_wireframe(vnf);
Example 4: Open shape made from a three arcs, with col_wrap=true.
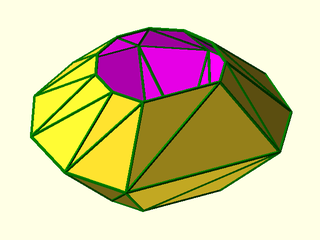
include <BOSL2/std.scad>
rows = [
for(h=[-20:20:20])
path3d(arc(r=40-abs(h), angle=280, 10), h)
];
vnf = vnf_vertex_array(rows, reverse=true, col_wrap=true);
vnf_polyhedron(vnf);
color("green") vnf_wireframe(vnf);
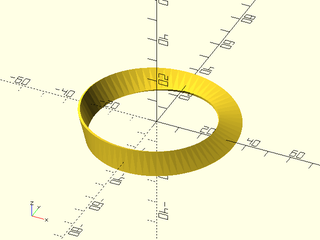
Example 5: Open shape made from a three arcs, with caps=true and col_wrap=true.
include <BOSL2/std.scad>
rows = [
for(h=[-20:20:20])
path3d(arc(r=40-abs(h), angle=280, 10), h)
];
vnf = vnf_vertex_array(rows, reverse=true, caps=true, col_wrap=true);
vnf_polyhedron(vnf);
color("green") vnf_wireframe(vnf);
Example 6: Both col_wrap and row_wrap are true to make a torus.
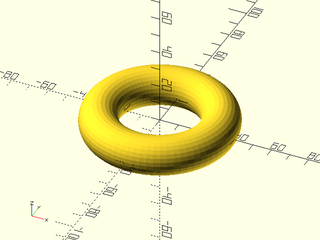
include <BOSL2/std.scad>
vnf = vnf_vertex_array(
points=[
for (a=[0:5:360-EPSILON])
apply(
zrot(a) * right(30) * xrot(90),
path3d(circle(d=20))
)
],
col_wrap=true, row_wrap=true, reverse=true
);
vnf_polyhedron(vnf);
Example 7: Möbius Strip. Note that row_wrap is not used, and the first and last profile copies are the same.
include <BOSL2/std.scad>
vnf = vnf_vertex_array(
points=[
for (a=[0:5:360]) apply(
zrot(a) * right(30) * xrot(90) * zrot(a/2+60),
path3d(square([1,10], center=true))
)
],
col_wrap=true, reverse=true
);
vnf_polyhedron(vnf);
Example 8: Assembling a Polyhedron from Multiple Parts
include <BOSL2/std.scad>
wall_points = [
for (a = [-90:2:90]) apply(
up(a) * scale([1-0.1*cos(a*6),1-0.1*cos((a+90)*6),1]),
path3d(circle(d=100))
)
];
cap = [
for (a = [0:0.01:1+EPSILON]) apply(
up(90-5*sin(a*360*2)) * scale([a,a,1]),
wall_points[0]
)
];
cap1 = [for (p=cap) down(90, p=zscale(-1, p=p))];
cap2 = [for (p=cap) up(90, p=p)];
vnf1 = vnf_vertex_array(points=wall_points, col_wrap=true);
vnf2 = vnf_vertex_array(points=cap1, col_wrap=true);
vnf3 = vnf_vertex_array(points=cap2, col_wrap=true, reverse=true);
vnf_polyhedron([vnf1, vnf2, vnf3]);
Example 9: Building a Multi-Stage Cylindrical Ramp
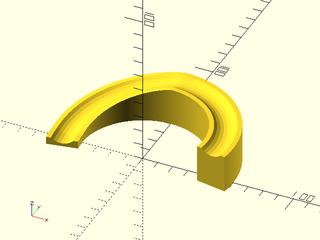
include <BOSL2/std.scad>
include <BOSL2/rounding.scad>
major_r = 50;
groove_profile = [
[-10,0], each arc(points=[[-7,0],[0,-3],[7,0]]), [10,0]
];
ramp_profile = [ [-10,25], [90,25], [180,5], [190,5] ];
rgroove = apply(right(major_r) * xrot(90), path3d(groove_profile));
rprofile = round_corners(ramp_profile, radius=20, closed=false, $fn=72);
vnf = vnf_vertex_array([
for (a = [ramp_profile[0].x : 1 : last(ramp_profile).x]) let(
z = lookup(a,rprofile),
m = zrot(a) * up(z)
)
apply(m, [ [rgroove[0].x,0,-z], each rgroove, [last(rgroove).x,0,-z] ])
], caps=true, col_wrap=true, reverse=true);
vnf_polyhedron(vnf, convexity=8);
Function: vnf_tri_array()
Synopsis: Returns a VNF from an array of points. The array need not be rectangular. [VNF]
Topics: VNF Generators, Lists
See Also: vnf_vertex_array(), vnf_join(), vnf_from_polygons(), vnf_merge_points()
Usage:
- vnf = vnf_tri_array(points, [caps=], [cap1=], [cap2=], [reverse=], [col_wrap=], [row_wrap=])
Description:
Produces a VNF from an array of points where each row length can differ from the adjacent rows by any amount. This enables the construction of triangular or even irregular VNF patches. The resulting VNF can be wrapped along the rows by setting row_wrap to true, and wrapped along columns by setting col_wrap to true. It is possible to do both at once.
If row_wrap is false or not provided, end caps can be generated across the top and/or bottom rows.
The algorithm starts with the first point on each row and recursively walks around finding the minimum-length edge to make each new triangle face. This may result in several triangles being connected to one vertex. When triangulating two rows that happen to be equal length, the result is equivalent to vnf_vertex_array() using the "min_edge" style. If you already have a rectangular vertex list (equal length rows), you should use vnf_vertex_array() if you need a different triangulation style.
If you need to merge two VNF arrays that share edges using vnf_join() you can remove the duplicated vertices using vnf_merge_points().
Arguments:
| By Position | What it does |
|---|---|
points |
List of point lists for each row. |
| By Name | What it does |
|---|---|
caps |
If true, add endcap faces to the first and last rows. |
cap1 |
If true, add an endcap face to the first row. |
cap2 |
If true, add an endcap face to the last row. |
col_wrap |
If true, add faces to connect the last column to the first. |
row_wrap |
If true, add faces to connect the last row to the first. |
reverse |
If true, reverse all face normals. |
Example 1: Each row has one more point than the preceeding one.
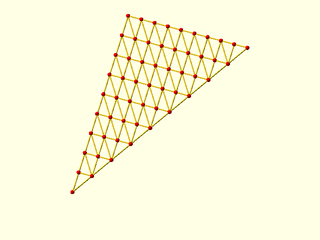
include <BOSL2/std.scad>
pts = [for(y=[1:1:10]) [for(x=[0:y-1]) [x,y,y]]];
vnf = vnf_tri_array(pts);
vnf_wireframe(vnf,width=0.1);
color("red")move_copies(flatten(pts)) sphere(r=.15,$fn=9);
Example 2: Each row has two more points than the preceeding one.
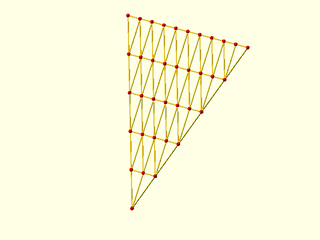
include <BOSL2/std.scad>
pts = [for(y=[0:2:10]) [for(x=[-y/2:y/2]) [x,y,y]]];
vnf = vnf_tri_array(pts);
vnf_wireframe(vnf,width=0.1);
color("red")move_copies(flatten(pts)) sphere(r=.15,$fn=9);
Example 3: Merging two VNFs to construct a cone with one point length change between rows.
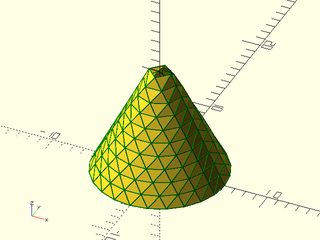
include <BOSL2/std.scad>
pts1 = [for(z=[0:10]) path3d(arc(3+z,r=z/2+1, angle=[0,180]),10-z)];
pts2 = [for(z=[0:10]) path3d(arc(3+z,r=z/2+1, angle=[180,360]),10-z)];
vnf = vnf_join([vnf_tri_array(pts1),
vnf_tri_array(pts2)]);
color("green")vnf_wireframe(vnf,width=0.1);
vnf_polyhedron(vnf);
Example 4: Cone with length change two between rows
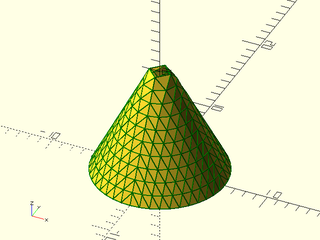
include <BOSL2/std.scad>
pts1 = [for(z=[0:1:10]) path3d(arc(3+2*z,r=z/2+1, angle=[0,180]),10-z)];
pts2 = [for(z=[0:1:10]) path3d(arc(3+2*z,r=z/2+1, angle=[180,360]),10-z)];
vnf = vnf_join([vnf_tri_array(pts1),
vnf_tri_array(pts2)]);
color("green")vnf_wireframe(vnf,width=0.1);
vnf_polyhedron(vnf);
Example 5: The number of points per row can change irregularly by any amount.
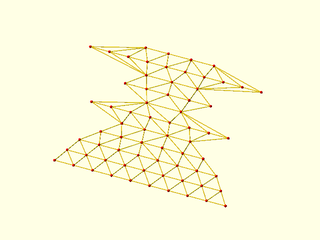
include <BOSL2/std.scad>
lens = [10,9,8,6,4,8,2,5,3,10,4];
pts = [for(y=idx(lens)) lerpn([-lens[y],y,y],[lens[y],y,y],lens[y])];
vnf = vnf_tri_array(pts);
vnf_wireframe(vnf,width=0.1);
color("red")move_copies(flatten(pts)) sphere(r=.15,$fn=9);
Example 6: Model of a cymbal with roughly same-size facets, using a different number of points for each concentric ring of vertices.
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [
[[0,26], [35,26], [29,0], [80,16], [102,0]], //top
[[99,-1], [79,15], [28,-1], [34,25], [-1,25]] // bottom
];
points = [
for(b=bez)
for(u=[0.01:0.04:1]) let(
bzp = bezier_points(b,u),
r = bzp[0],
n = max(3, round(360 / (6/r * 180/PI)))
) path3d(regular_ngon(n, r=r), bzp[1])
];
vnf = vnf_tri_array(points, reverse=true, col_wrap=true, caps=true);
color("brown") difference() {
vnf_polyhedron(vnf);
cylinder(30, d=8);
}
Function: vnf_join()
Synopsis: Returns a single VNF structure from a list of VNF structures. [VNF]
Topics: VNF Generators, Lists
See Also: vnf_tri_array(), vnf_vertex_array(), vnf_from_polygons(), vnf_from_region()
Usage:
- vnf = vnf_join([VNF, VNF, VNF, ...]);
Description:
Given a list of VNF structures, merges them all into a single VNF structure.
Combines all the points of the input VNFs and labels the faces appropriately.
All the points in the input VNFs will appear in the output, even if they are
duplicates of each other. It is valid to repeat points in a VNF, but if you
with to remove the duplicates that will occur along joined edges, use vnf_merge_points().
Note that this is a tool for manipulating polyhedron data. It is for building up a full polyhedron from partial polyhedra. It is not a union operator for VNFs. The VNFs to be joined must not intersect each other, except at edges, or the result will be an invalid polyhedron. Similarly the result must not have any other illegal polyhedron characteristics, such as creating more than two faces sharing the same edge. If you want a valid result it is your responsibility to ensure that the polyhedron has no holes, no intersecting faces or edges, and obeys all the requirements that CGAL expects.
For example, if you combine two pyramids to try to make an octahedron, the result will be invalid because of the two internal faces created by the pyramid bases. A valid use would be to build a cube missing one face and a pyramid missing its base and then join them into a cube with a point.
Arguments:
| By Position | What it does |
|---|---|
vnfs |
a list of the VNFs to joint into one VNF. |
Example 1: Here is a VNF where the top face is missing. It is not a valid polyhedron like this, but we can use it as a building block to make a polyhedron.
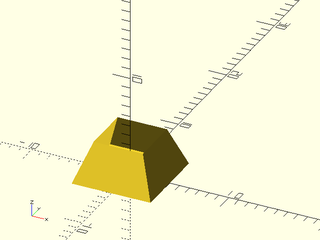
include <BOSL2/std.scad>
bottom = vnf_vertex_array([path3d(rect(8)), path3d(rect(5),4)],col_wrap=true,cap1=true);
vnf_polyhedron(bottom);
Example 2: Here is a VNF that also has a missing face.
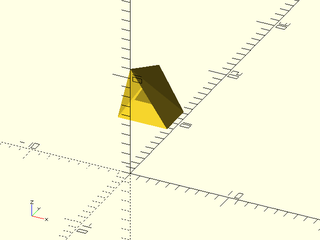
include <BOSL2/std.scad>
triangle = yrot(-90,path3d(regular_ngon(n=3,side=5,anchor=LEFT)));
top = up(4,vnf_vertex_array([list_set(right(2.5,triangle),0,[0,0,7]),
right(6,triangle)
], col_wrap=true, cap2=true));
vnf_polyhedron(zrot(90,top));
Example 3: Using vnf_join combines the two VNFs into a single VNF. Note that they share an edge. But the result still isn't closed, so it is not yet a valid polyhedron.
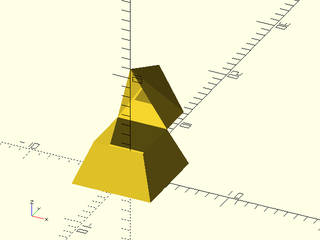
include <BOSL2/std.scad>
bottom = vnf_vertex_array([path3d(rect(8)), path3d(rect(5),4)],col_wrap=true,cap1=true);
triangle = yrot(-90,path3d(regular_ngon(n=3,side=5,anchor=LEFT)));
top = up(4,vnf_vertex_array([list_set(right(2.5,triangle),0,[0,0,7]),
right(6,triangle)
], col_wrap=true, cap2=true));
full = vnf_join([bottom,zrot(90,top)]);
vnf_polyhedron(full);
Example 4: If we add enough pieces, and the pieces are all consistent with each other, then we can arrive at a valid polyhedron like this one. To be valid you need to meet all the CGAL requirements: every edge has exactly two faces, all faces are in clockwise order, no intersections of edges.
include <BOSL2/std.scad>
bottom = vnf_vertex_array([path3d(rect(8)), path3d(rect(5),4)],col_wrap=true,cap1=true);
triangle = yrot(-90,path3d(regular_ngon(n=3,side=5,anchor=LEFT)));
top = up(4,vnf_vertex_array([list_set(right(2.5,triangle),0,[0,0,7]),
right(6,triangle)
], col_wrap=true, cap2=true));
full = vnf_join([bottom,
for(theta=[0:90:359]) zrot(theta,top)
]);
vnf_polyhedron(full);
Example 5: The vnf_join function is not a union operator for polyhedra. If any faces intersect, like they do in this example where we combine the faces of two cubes, the result is invalid and will give rise to CGAL errors when you add more objects into the model.
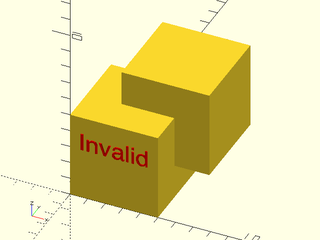
include <BOSL2/std.scad>
cube1 = cube(5);
cube2 = move([2,2,2],cube1);
badvnf = vnf_join([cube1,cube2]);
vnf_polyhedron(badvnf);
right(2.5)up(3)color("red")
text3d("Invalid",size=1,anchor=CENTER,
orient=FRONT,h=.1);
Function: vnf_from_polygons()
Synopsis: Returns a VNF from a list of 3D polygons. [VNF]
Topics: VNF Generators, Lists
See Also: vnf_tri_array(), vnf_join(), vnf_vertex_array(), vnf_from_region()
Usage:
- vnf = vnf_from_polygons(polygons, [eps]);
Description:
Given a list of 3D polygons, produces a VNF containing those polygons.
It is up to the caller to make sure that the points are in the correct order to make the face
normals point outwards. No checking for duplicate vertices is done. If you want to
remove duplicate vertices use vnf_merge_points(). Polygons with zero area are discarded from the face list by default.
If you give non-coplanar faces an error is displayed. These checks increase run time by about 2x for triangular polygons, but
about 10x for pentagons; the checks can be disabled by setting fast=true.
Arguments:
| By Position | What it does |
|---|---|
polygons |
The list of 3D polygons to turn into a VNF |
fast |
Set to true to skip area and coplanarity checks for increased speed. Default: false |
eps |
Polygons with area smaller than this are discarded. Default: EPSILON |
Example 1: Construction of a dodecahedron from pentagon faces.
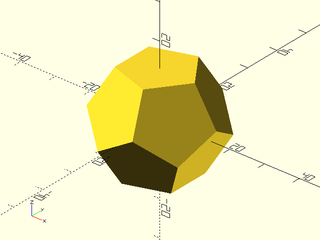
include <BOSL2/std.scad>
dihedral = 2*atan(PHI); // dodecahedron face dihedral
rpenta = 10; // pentagon face radius
edge = 2*rpenta*sin(36); // edge length
inrad = 0.5*edge * PHI*PHI/sqrt(3-PHI); // inner radius
face3d = path3d(pentagon(rpenta), inrad); // single face
facepoints = [
face3d,
for(a=[36:72:360]) zrot(a, yrot(180-dihedral, face3d)),
for(a=[36:72:360]) zrot(a, yrot(360-dihedral, face3d)),
yrot(180, face3d)
];
vnf = vnf_from_polygons(facepoints, fast=true);
vnf_polyhedron(vnf);
Function: vnf_from_region()
Synopsis: Returns a 3D VNF given a 2D region. [VNF]
Topics: VNF Generators, Lists
See Also: vnf_vertex_array(), vnf_tri_array(), vnf_join(), vnf_from_polygons()
Usage:
- vnf = vnf_from_region(region, [transform], [reverse]);
Description:
Given a (two-dimensional) region, applies the given transformation matrix to it and makes a (three-dimensional) triangulated VNF of faces for that region, reversed if desired.
Arguments:
| By Position | What it does |
|---|---|
region |
The region to convert to a vnf. |
transform |
If given, a transformation matrix to apply to the faces generated from the region. Default: No transformation applied. |
reverse |
If true, reverse the normals of the faces generated from the region. An untransformed region will have face normals pointing UP. Default: false |
Example 1:
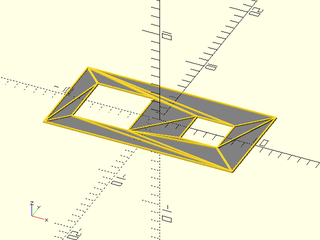
include <BOSL2/std.scad>
region = [square([20,10],center=true),
right(5,square(4,center=true)),
left(5,square(6,center=true))];
vnf = vnf_from_region(region);
color("gray")down(.125)
linear_extrude(height=.125)region(region);
vnf_wireframe(vnf,width=.25);
Section: VNF Testing and Access
Function: is_vnf()
Synopsis: Returns true given a VNF-like structure.
Topics: VNF Manipulation
See Also: is_vnf_list(), vnf_vertices(), vnf_faces()
Usage:
- bool = is_vnf(x);
Description:
Returns true if the given value looks like a VNF structure.
Function: is_vnf_list()
Synopsis: Returns true given a list of VNF-like structures.
Topics: VNF Manipulation
See Also: is_vnf(), vnf_vertices(), vnf_faces()
Description:
Returns true if the given value looks passingly like a list of VNF structures.
Function: vnf_vertices()
Synopsis: Returns the list of vertex points from a VNF.
Topics: VNF Manipulation
See Also: is_vnf(), is_vnf_list(), vnf_faces()
Description:
Given a VNF structure, returns the list of vertex points.
Function: vnf_faces()
Synopsis: Returns the list of faces from a VNF.
Topics: VNF Manipulation
See Also: is_vnf(), is_vnf_list(), vnf_vertices()
Description:
Given a VNF structure, returns the list of faces, where each face is a list of indices into the VNF vertex list.
Section: Altering the VNF Internals
Function: vnf_reverse_faces()
Synopsis: Reverses the faces of a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_quantize(), vnf_merge_points(), vnf_drop_unused_points(), vnf_triangulate(), vnf_slice(), vnf_unify_faces()
Usage:
- rvnf = vnf_reverse_faces(vnf);
Description:
Reverses the orientation of all the faces in the given VNF.
Function: vnf_quantize()
Synopsis: Quantizes the vertex coordinates of a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_merge_points(), vnf_drop_unused_points(), vnf_triangulate(), vnf_slice()
Usage:
- vnf2 = vnf_quantize(vnf,[q]);
Description:
Quantizes the vertex coordinates of the VNF to the given quanta q.
Arguments:
| By Position | What it does |
|---|---|
vnf |
The VNF to quantize. |
q |
The quanta to quantize the VNF coordinates to. |
Function: vnf_merge_points()
Synopsis: Consolidates duplicate vertices of a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_quantize(), vnf_drop_unused_points(), vnf_triangulate(), vnf_slice(), vnf_unify_faces()
Usage:
- new_vnf = vnf_merge_points(vnf, [eps]);
Description:
Given a VNF, consolidates all duplicate vertices with a tolerance eps, relabeling the faces as necessary,
and eliminating any face with fewer than 3 vertices. Unreferenced vertices of the input VNF are not dropped.
To remove such vertices uses vnf_drop_unused_points().
Arguments:
| By Position | What it does |
|---|---|
vnf |
a VNF to consolidate |
eps |
the tolerance in finding duplicates. Default: EPSILON |
Function: vnf_drop_unused_points()
Synopsis: Removes unreferenced vertices from a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_quantize(), vnf_merge_points(), vnf_triangulate(), vnf_slice(), vnf_unify_faces()
Usage:
- clean_vnf = vnf_drop_unused_points(vnf);
Description:
Remove all unreferenced vertices from a VNF. Note that in most cases unreferenced vertices cause no harm, and this function may be slow on large VNFs.
Function: vnf_triangulate()
Synopsis: Triangulates the faces of a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_quantize(), vnf_merge_points(), vnf_drop_unused_points(), vnf_slice(), vnf_unify_faces()
Usage:
- vnf2 = vnf_triangulate(vnf);
Description:
Triangulates faces in the VNF that have more than 3 vertices.
Arguments:
| By Position | What it does |
|---|---|
vnf |
VNF to triangulate |
Example 1:
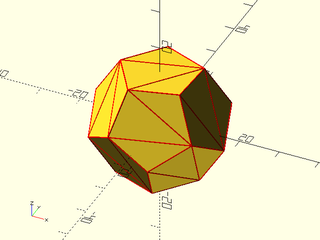
include <BOSL2/std.scad>
include <BOSL2/polyhedra.scad>
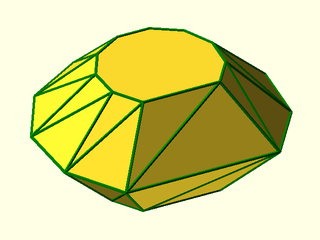
vnf = zrot(33,regular_polyhedron_info("vnf", "dodecahedron", side=12));
vnf_polyhedron(vnf);
triangulated = vnf_triangulate(vnf);
color("red")vnf_wireframe(triangulated,width=.3);
Function: vnf_unify_faces()
Synopsis: Remove triangulation from VNF, returning a copy with full faces [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_quantize(), vnf_merge_points(), vnf_triangulate(), vnf_slice()
Usage:
- newvnf = vnf_unify_faces(vnf);
Description:
When a VNF has been triangulated, the polygons that form the true faces have been chopped up into triangles. This can create problems for algorithms that operate on the VNF itself, where you might want to be able to identify the true faces. This function merges together the triangles that form those true faces, turning a VNF where each true face is represented by a single entry in the faces list of the VNF. This function requires that the true faces have no internal vertices. This will always be true for a triangulated VNF, but might fail for a VNF with some other face partition. If internal vertices are present, the output will include backtracking paths from the boundary to all of those vertices.
Arguments:
| By Position | What it does |
|---|---|
vnf |
vnf whose faces you want to unify |
Example 1: Original prism on the left is triangulated. On the right, the result of unifying the faces.
include <BOSL2/std.scad>
$fn=16;
poly = linear_sweep(hexagon(side=10),h=35);
vnf = vnf_unify_faces(poly);
vnf_wireframe(poly);
color([0,1,1,.70])vnf_polyhedron(poly);
right(25){
vnf_wireframe(vnf);
color([0,1,1,.70])vnf_polyhedron(vnf);
}
Function: vnf_slice()
Synopsis: Slice the faces of a VNF along an axis. [VNF]
Topics: VNF Manipulation
See Also: vnf_reverse_faces(), vnf_quantize(), vnf_merge_points(), vnf_drop_unused_points(), vnf_triangulate()
Usage:
- sliced = vnf_slice(vnf, dir, cuts);
Description:
Slice the faces of a VNF along a specified axis direction at a given list of cut points. The cut points can appear in any order. You can use this to refine the faces of a VNF before applying a nonlinear transformation to its vertex set.
Arguments:
| By Position | What it does |
|---|---|
vnf |
VNF to slice |
dir |
normal direction to the slices, either "X", "Y" or "Z" |
cuts |
X, Y or Z values where cuts occur |
Example 1:
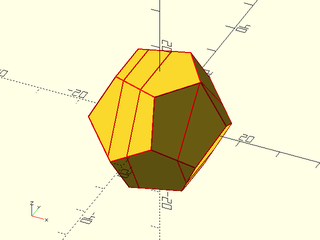
include <BOSL2/std.scad>
include <BOSL2/polyhedra.scad>
vnf = regular_polyhedron_info("vnf", "dodecahedron", side=12);
vnf_polyhedron(vnf);
sliced = vnf_slice(vnf, "X", [-6,-1,10]);
color("red")vnf_wireframe(sliced,width=.3);
Section: Turning a VNF into geometry
Module: vnf_polyhedron()
Synopsis: Returns a polyhedron from a VNF or list of VNFs. [Geom]
Topics: VNF Manipulation
See Also: vnf_wireframe()
Usage:
- vnf_polyhedron(vnf) [ATTACHMENTS];
- vnf_polyhedron([VNF, VNF, VNF, ...]) [ATTACHMENTS];
Description:
Given a VNF structure, or a list of VNF structures, creates a polyhedron from them.
Arguments:
| By Position | What it does |
|---|---|
vnf |
A VNF structure, or list of VNF structures. |
convexity |
Max number of times a line could intersect a wall of the shape. |
cp |
Centerpoint for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid" |
anchor |
Translate so anchor point is at origin (0,0,0). See anchor. Default: "origin" |
spin |
Rotate this many degrees around the Z axis after anchor. See spin. Default: 0 |
orient |
Vector to rotate top towards, after spin. See orient. Default: UP |
atype |
Select "hull" or "intersect" anchor type. Default: "hull" |
Anchor Types:
| Anchor Type | What it is |
|---|---|
| "hull" | Anchors to the virtual convex hull of the shape. |
| "intersect" | Anchors to the surface of the shape. |
Named Anchors:
| Anchor Name | Position |
|---|---|
| "origin" | Anchor at the origin, oriented UP. |
Module: vnf_wireframe()
Synopsis: Creates a wireframe model from a VNF. [VNF]
Topics: VNF Manipulation
See Also: vnf_polyhedron()
Usage:
- vnf_wireframe(vnf, [width]);
Description:
Given a VNF, creates a wire frame ball-and-stick model of the polyhedron with a cylinder for each edge and a sphere at each vertex. The width parameter specifies the width of the sticks that form the wire frame and the diameter of the balls.
Arguments:
| By Position | What it does |
|---|---|
vnf |
A vnf structure |
width |
width of the cylinders forming the wire frame. Default: 1 |
Example 1:
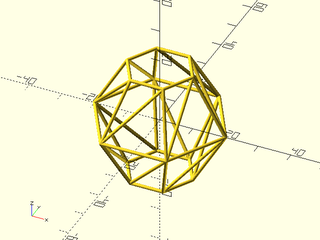
include <BOSL2/std.scad>
$fn=32;
ball = sphere(r=20, $fn=6);
vnf_wireframe(ball,width=1);
Example 2:
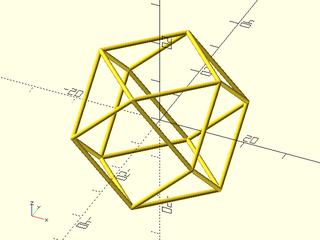
include <BOSL2/std.scad>
include <BOSL2/polyhedra.scad>
$fn=32;
cube_oct = regular_polyhedron_info("vnf",
name="cuboctahedron", or=20);
vnf_wireframe(cube_oct);
Example 3: The spheres at the vertex are imperfect at aligning with the cylinders, so especially at low $fn things look prety ugly. This is normal.
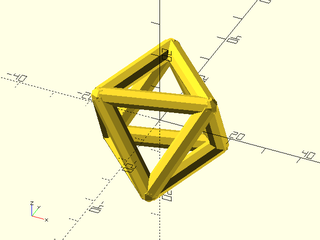
include <BOSL2/std.scad>
include <BOSL2/polyhedra.scad>
$fn=8;
octahedron = regular_polyhedron_info("vnf",
name="octahedron", or=20);
vnf_wireframe(octahedron,width=5);
Section: Operations on VNFs
Function: vnf_volume()
Synopsis: Returns the volume of a VNF.
Topics: VNF Manipulation
See Also: vnf_area(), vnf_halfspace(), vnf_bend()
Usage:
- vol = vnf_volume(vnf);
Description:
Returns the volume enclosed by the given manifold VNF. The VNF must describe a valid polyhedron with consistent face direction and no holes; otherwise the results are undefined. Returns a positive volume if face direction is clockwise and a negative volume if face direction is counter-clockwise.
Function: vnf_area()
Synopsis: Returns the surface area of a VNF.
Topics: VNF Manipulation
See Also: vnf_volume(), vnf_halfspace(), vnf_bend()
Usage:
- area = vnf_area(vnf);
Description:
Returns the surface area in any VNF by adding up the area of all its faces. The VNF need not be a manifold.
Function: projection()
Synopsis: Returns projection or intersection of vnf with XY plane [VNF]
Topics: VNF Manipulation
See Also: vnf_halfspace()
Usage:
- region = projection(vnf, [cut]);
Description:
When cut=false, which is the default, projects the input VNF
onto the XY plane, returning a region. Note that as currently implemented, this operation
involves the 2D union of all the projected faces and can be very
slow if the VNF has many faces. Minimize the face count of the VNF for best performance.
When cut=true, returns the intersection of the VNF with the
XY plane, which is again a region. If the VNF does not intersect
the XY plane then returns the empty set. This operation is
much faster than cut=false.
Example 1: Here's a VNF with two linked toruses and a small cube
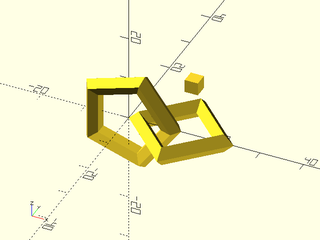
include <BOSL2/std.scad>
vnf = vnf_join([
xrot(90,torus(id=15,od=24,$fn=5)),
right(12,torus(id=15,od=24,$fn=4)),
up(13,right(15,cube(3,center=true)))
]);
vnf_polyhedron(vnf);
Example 2: Projection of above VNF with default behavior, cut=false
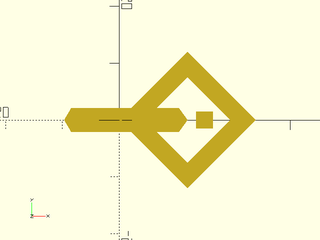
include <BOSL2/std.scad>
vnf = vnf_join([
xrot(90,torus(id=15,od=24,$fn=5)),
right(12,torus(id=15,od=24,$fn=4)),
up(13,right(15,cube(3,center=true)))
]);
reg = projection(vnf);
region(reg);
Example 3: Tilted torus
include <BOSL2/std.scad>
vnf = xrot(35,torus(id=4,od=12,$fn=32));
vnf_polyhedron(vnf);
Example 4: Projection of tilted torus using cut=true
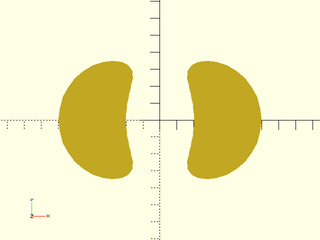
include <BOSL2/std.scad>
vnf = xrot(35,torus(id=4,od=12,$fn=32));
reg = projection(vnf,cut=true);
region(reg);
Function: vnf_halfspace()
Synopsis: Returns the intersection of the vnf with a half space. [VNF]
Topics: VNF Manipulation
See Also: vnf_volume(), vnf_area(), vnf_bend()
Usage:
- newvnf = vnf_halfspace(plane, vnf, [closed], [boundary]);
Description:
Returns the intersection of the vnf with a half space. The half space is defined by
plane = [A,B,C,D], taking the side where the normal [A,B,C] points: Ax+By+Cz≥D.
If closed is set to false then the cut face is not included in the vnf. This could
allow further extension of the vnf by join with other vnfs using vnf_join().
Note that if your given VNF has holes (missing faces) or is not a complete polyhedron
then closed=true is may produce invalid results when it tries to construct closing faces
on the cut plane. Set closed=false for such inputs.
If you set boundary to true then the return will be the pair [vnf,boundary] where vnf is the
vnf as usual (with closed=false) and boundary is a list giving each connected component of the cut
boundary surface. Each entry in boundary is a list of index values that index into the vnf vertex list (vnf[0]).
This makes it possible to construct mating shapes, e.g. with skin() or vnf_vertex_array() that
can be combined using vnf_join() to make a valid polyhedron.
Note that the input to vnf_halfspace() does not need to be a closed, manifold polyhedron. Because it adds the faces on the cut surface, you can use vnf_halfspace() to cap off an open shape if you slice through a region that excludes all of the gaps in the input VNF.
Arguments:
| By Position | What it does |
|---|---|
plane |
plane defining the boundary of the half space |
vnf |
VNF to cut |
closed |
if false do not return the cut face(s) in the returned VNF. Default: true |
boundary |
if true return a pair [vnf,boundary] where boundary is a list of paths on the cut boundary indexed into the VNF vertex list. If boundary is true, then closed is set to false. Default: false |
Example 1:
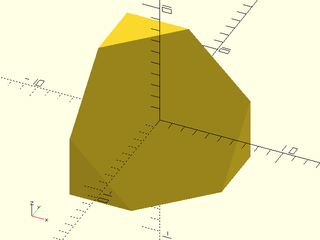
include <BOSL2/std.scad>
vnf = cube(10,center=true);
cutvnf = vnf_halfspace([-1,1,-1,0], vnf);
vnf_polyhedron(cutvnf);
Example 2: Cut face has 2 components
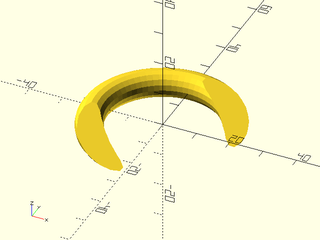
include <BOSL2/std.scad>
vnf = path_sweep(circle(r=4, $fn=16),
circle(r=20, $fn=64),closed=true);
cutvnf = vnf_halfspace([-1,1,-4,0], vnf);
vnf_polyhedron(cutvnf);
Example 3: Cut face is not simply connected
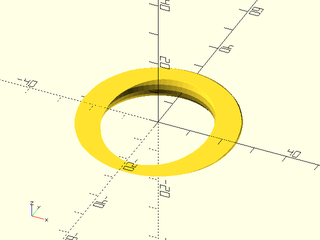
include <BOSL2/std.scad>
vnf = path_sweep(circle(r=4, $fn=16),
circle(r=20, $fn=64),closed=true);
cutvnf = vnf_halfspace([0,0.7,-4,0], vnf);
vnf_polyhedron(cutvnf);
Example 4: Cut object has multiple components
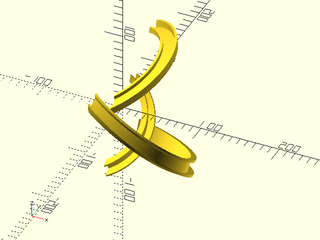
include <BOSL2/std.scad>
function knot(a,b,t) = // rolling knot
[ a * cos (3 * t) / (1 - b* sin (2 *t)),
a * sin( 3 * t) / (1 - b* sin (2 *t)),
1.8 * b * cos (2 * t) /(1 - b* sin (2 *t))];
a = 0.8; b = sqrt (1 - a * a);
ksteps = 400;
knot_path = [for (i=[0:ksteps-1]) 50 * knot(a,b,(i/ksteps)*360)];
ushape = [[-10, 0],[-10, 10],[ -7, 10],[ -7, 2],[ 7, 2],[ 7, 7],[ 10, 7],[ 10, 0]];
knot=path_sweep(ushape, knot_path, closed=true, method="incremental");
cut_knot = vnf_halfspace([1,0,0,0], knot);
vnf_polyhedron(cut_knot);
Example 5: Cut a sphere with an arbitrary plane
include <BOSL2/std.scad>
vnf1=sphere(r=50, style="icosa", $fn=16);
vnf2=vnf_halfspace([.8,1,-1.5,0], vnf1);
vnf_polyhedron(vnf2);
Example 6: Cut it again, but with closed=false to leave an open boundary.
include <BOSL2/std.scad>
vnf1=sphere(r=50, style="icosa", $fn=16);
vnf2=vnf_halfspace([.8,1,-1.5,0], vnf1);
vnf3=vnf_halfspace([0,0,-1,0], vnf2, closed=false);
vnf_polyhedron(vnf3);
Example 7: Use {vnf_join()} to combine with a mating vnf, in this case a reflection of the part we made.
include <BOSL2/std.scad>
vnf1=sphere(r=50, style="icosa", $fn=16);
vnf2=vnf_halfspace([.8,1,-1.5,0], vnf1);
vnf3=vnf_halfspace([0,0,-1,0], vnf2, closed=false);
vnf4=vnf_join([vnf3, zflip(vnf3,1)]);
vnf_polyhedron(vnf4);
Example 8: When the input VNF is a surface with a boundary, if you use the default setting closed=true, then vnf_halfspace() tries to construct closing faces from the edges created by the cut. These faces may be invalid, for example if the cut points are collinear. In this example the constructed face is a valid face.
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch=[
[[10,-10,0],[1,-1,0],[-1,-1,0],[-10,-10,0]],
[[10,-10,20],[1,-1,20],[-1,-1,20],[-10,-10,20]]
];
vnf=bezier_vnf(patch);
vnfcut = vnf_halfspace([-.8,0,-1,-14],vnf);
vnf_polyhedron(vnfcut);
Example 9: Setting closed to false eliminates this (possibly invalid) face:
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch=[
[[10,-10,0],[1,-1,0],[-1,-1,0],[-10,-10,0]],
[[10,-10,20],[1,-1,20],[-1,-1,20],[-10,-10,20]]
];
vnf=bezier_vnf(patch);
vnfcut = vnf_halfspace([-.8,0,-1,-14],vnf,closed=false);
vnf_polyhedron(vnfcut);
Example 10: Here is a VNF that has holes, so it is not a valid manifold.
include <BOSL2/std.scad>
outside = linear_sweep(circle(r=30), h=100, caps=false);
inside = yrot(7,linear_sweep(circle(r=10), h=120, caps=false));
open_vnf=vnf_join([outside, vnf_reverse_faces(inside)]);
vnf_polyhedron(open_vnf);
Example 11: By cutting it at each end we can create closing faces, resulting in a valid manifold without holes.
include <BOSL2/std.scad>
outside = linear_sweep(circle(r=30), h=100, caps=false);
inside = yrot(11,linear_sweep(circle(r=10), h=120, caps=false));
open_vnf=vnf_join([outside, vnf_reverse_faces(inside)]);
vnf = vnf_halfspace([0,0,1,5], vnf_halfspace([0,.7,-1,-75], open_vnf));
vnf_polyhedron(vnf);
Example 12: If boundary=true then the return is a list with the VNF and boundary data.
include <BOSL2/std.scad>
vnf = path_sweep(circle(r=4, $fn=16),
circle(r=20, $fn=64),closed=true);
cut_bnd = vnf_halfspace([-1,1,-4,0], vnf, boundary=true);*/
cutvnf = cut_bnd[0];
boundary = [for(b=cut_bnd[1]) select(cutvnf[0],b)];
vnf_polyhedron(cutvnf);
stroke(boundary,color="red");
Function: vnf_bend()
Synopsis: Bends a VNF around an axis. [VNF]
Topics: VNF Manipulation
See Also: vnf_volume(), vnf_area(), vnf_halfspace()
Usage:
- bentvnf = vnf_bend(vnf,r|d=,[axis=]);
Description:
Bend a VNF around the X, Y or Z axis, splitting up faces as necessary. Returns the bent
VNF. For bending around the Z axis the input VNF must not cross the Y=0 plane. For bending
around the X or Y axes the VNF must not cross the Z=0 plane. Note that if you wrap a VNF all the way around
it may intersect itself, which produces an invalid polyhedron. It is your responsibility to
avoid this situation. The 1:1
radius is where the curved length of the bent VNF matches the length of the original VNF. If the
r or d arguments are given, then they will specify the 1:1 radius or diameter. If they are
not given, then the 1:1 radius will be defined by the distance of the furthest vertex in the
original VNF from the Z=0 plane. You can adjust the granularity of the bend using the standard
$fa, $fs, and $fn variables.
Arguments:
| By Position | What it does |
|---|---|
vnf |
The original VNF to bend. |
r |
If given, the radius where the size of the original shape is the same as in the original. |
| By Name | What it does |
|---|---|
d |
If given, the diameter where the size of the original shape is the same as in the original. |
axis |
The axis to wrap around. "X", "Y", or "Z". Default: "Z" |
Example 1:
include <BOSL2/std.scad>
vnf0 = cube([100,40,10], center=true);
vnf1 = up(50, p=vnf0);
vnf2 = down(50, p=vnf0);
bent1 = vnf_bend(vnf1, axis="Y");
bent2 = vnf_bend(vnf2, axis="Y");
vnf_polyhedron([bent1,bent2]);
Example 2:
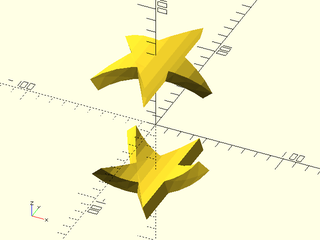
include <BOSL2/std.scad>
vnf0 = linear_sweep(star(n=5,step=2,d=100), height=10);
vnf1 = up(50, p=vnf0);
vnf2 = down(50, p=vnf0);
bent1 = vnf_bend(vnf1, axis="Y");
bent2 = vnf_bend(vnf2, axis="Y");
vnf_polyhedron([bent1,bent2]);
Example 3:
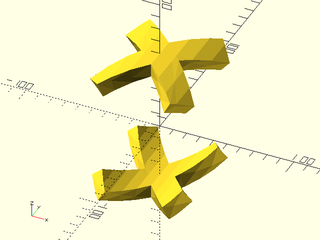
include <BOSL2/std.scad>
rgn = union(rect([100,20]),
rect([20,100]));
vnf0 = linear_sweep(zrot(45,p=rgn), height=10);
vnf1 = up(50, p=vnf0);
vnf2 = down(50, p=vnf0);
bent1 = vnf_bend(vnf1, axis="Y");
bent2 = vnf_bend(vnf2, axis="Y");
vnf_polyhedron([bent1,bent2]);
Example 4: Bending Around X Axis.
include <BOSL2/std.scad>
rgnr = union(
rect([20,100]),
back(50, p=trapezoid(w1=40, w2=0, h=20, anchor=FRONT))
);
vnf0 = xrot(00,p=linear_sweep(rgnr, height=10));
vnf1 = up(50, p=vnf0);
#vnf_polyhedron(vnf1);
bent1 = vnf_bend(vnf1, axis="X");
vnf_polyhedron([bent1]);
Example 5: Bending Around Y Axis.
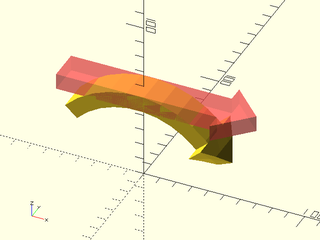
include <BOSL2/std.scad>
rgn = union(
rect([20,100]),
back(50, p=trapezoid(w1=40, w2=0, h=20, anchor=FRONT))
);
rgnr = zrot(-90, p=rgn);
vnf0 = xrot(00,p=linear_sweep(rgnr, height=10));
vnf1 = up(50, p=vnf0);
#vnf_polyhedron(vnf1);
bent1 = vnf_bend(vnf1, axis="Y");
vnf_polyhedron([bent1]);
Example 6: Bending Around Z Axis.
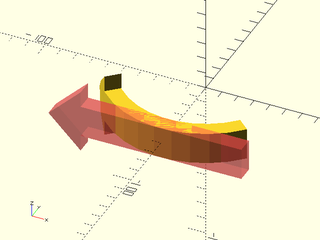
include <BOSL2/std.scad>
rgn = union(
rect([20,100]),
back(50, p=trapezoid(w1=40, w2=0, h=20, anchor=FRONT))
);
rgnr = zrot(90, p=rgn);
vnf0 = xrot(90,p=linear_sweep(rgnr, height=10));
vnf1 = fwd(50, p=vnf0);
#vnf_polyhedron(vnf1);
bent1 = vnf_bend(vnf1, axis="Z");
vnf_polyhedron([bent1]);
Example 7: Bending more than once around the cylinder
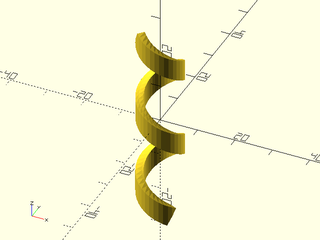
include <BOSL2/std.scad>
$fn=32;
vnf = apply(fwd(5)*yrot(30),cube([100,2,5],center=true));
bent = vnf_bend(vnf, axis="Z");
vnf_polyhedron(bent);
Function/Module: vnf_hull()
Synopsis: Compute convex hull of VNF or 3d path
Usage:
- vnf_hull = hull_vnf(vnf);
- hull_vnf(vnf,[fast]);
Description:
Given a VNF or a list of 3d points, compute the convex hull
and return it as a VNF. This differs from hull() and hull3d_faces() which
return just the face list referenced to the input point list. Note that the point
list that is returned will contain all the points that are actually used in the input
VNF, which may be many more points than are needed to represent the convex hull.
This is not usually a problem, but you can run the somewhat slow vnf_drop_unused_points()
function to fix this if necessary.
Arguments:
| By Position | What it does |
|---|---|
region |
region or path listing points to compute the hull from. |
fast |
(module only) if input is a point list (not a VNF) use a fasterer cheat that may handle more points, but could emit warnings. Ignored if input is a VNF. Default: false. |
Example 1: Input is a VNF
include <BOSL2/std.scad>
ellipse = xscale(2, p=circle($fn=48, r=3));
pentagon = subdivide_path(pentagon(r=1), 20);
vnf=path_sweep(pentagon, path3d(ellipse),
closed=true, twist=360*2);
vnfhull = vnf_hull(vnf);
vnf_polyhedron(vnf);
move([10,10])
vnf_polyhedron(vnfhull);
Example 2: Input is a point list
include <BOSL2/std.scad>
h=helix(l=40, turns=1, r=8);
color("red")move_copies(h)
sphere(r=0.5,$fn=12);
vnf_polyhedron(vnf_hull(h));
Function: vnf_boundary()
Synopsis: Returns the boundary of a VNF as an list of paths [VNF]
Topics: VNF Manipulation
See Also: vnf_halfspace(), vnf_merge_points()
Usage:
- boundary = vnf_boundary(vnf, [merge=], [idx=]);
Description:
Returns the boundary of a VNF as a list of paths. The input VNF must not contain duplicate points. By default, vnf_boundary() calls vnf_merge_points()
to remove duplicate points. Note, however, that this operation can be slow. If you are certain there are no duplicate points you can
set merge=false to disable the automatic point merge and save time. The result of running on a VNF with duplicate points is likely to
be incorrect or invalid; it may produce obscure errors.
The output will be a list of closed 3D paths. If the VNF has no boundary then the output is []. The boundary path(s) are
traversed in the same direction as the edges in the original VNF.
It is sometimes desirable to have the boundary available as an index list into the VNF vertex list. However, merging the points in the VNF changes the
VNF vertex point list. If you set merge=false you can also set idx=true to get an index list. As noted above, you must be certain
that your in put VNF has no duplicate vertices, perhaps by running vnf_merge_points() yourself on it. With idx=true
the output will be indices into the VNF vertex list, which enables you to associate the vertices on the boundary path with the original VNF.
Arguments:
| By Position | What it does |
|---|---|
vnf |
input vnf |
| By Name | What it does |
|---|---|
merge |
set to false to suppress the automatic invocation of vnf_merge_points(). Default: true |
idx |
if true, return indices into VNF vertices instead of actual 3D points. Must set merge=false to enable this. Default: false |
Example 1: In this example we know that the bezier patch VNF has no duplicate vertices, so we do not need to run vnf_merge_points().
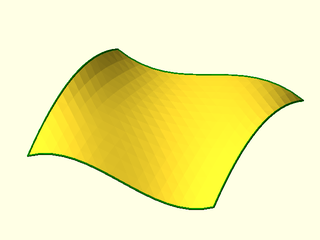
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
// u=0,v=0 u=1,v=0
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, -20], [50,-50, 0]],
[[-50,-16, 20], [-16,-16, 20], [ 16,-16, -20], [50,-16, 20]],
[[-50, 16, 20], [-16, 16, -20], [ 16, 16, 20], [50, 16, 20]],
[[-50, 50, 0], [-16, 50, -20], [ 16, 50, 20], [50, 50, 0]],
// u=0,v=1 u=1,v=1
];
bezvnf = bezier_vnf(patch);
boundary = vnf_boundary(bezvnf);
vnf_polyhedron(bezvnf);
stroke(boundary,color="green");
Example 2: An example with two path components on the boundary. The output from vnf_halfspace() can contain duplicate vertices, so we must invoke vnf_merge_points().
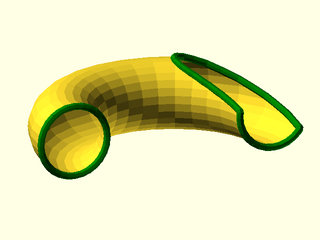
include <BOSL2/std.scad>
vnf = torus(id=20,od=40,$fn=28);
cutvnf=vnf_halfspace([0,1,0,0],
vnf_halfspace([-1,.5,-2.5,-12], vnf, closed=false),
closed=false);
vnf_polyhedron(cutvnf);
boundary = vnf_boundary(vnf_merge_points(cutvnf));
stroke(boundary,color="green");
Function: vnf_small_offset()
Synopsis: Computes an offset surface to a VNF for small offset distances [VNF]
Topics: VNF Manipulation
See Also: vnf_sheet(), vnf_merge_points()
Usage:
- newvnf = vnf(vnf, delta, [merge=]);
Description:
Computes a simple offset of a VNF by estimating the normal at every point based on the weighted average of surrounding polygons
in the mesh. The offset distance, delta, must be small enough so that no self-intersection occurs, which is no issue when the
curvature is positive (like the outside of a sphere) but for negative curvature it means the offset distance must be smaller
than the smallest radius of curvature of the VNF. If self-intersection
occurs, the resulting geometry will be invalid and you will get an error when you introduce a second object into the model.
It is your responsibility to avoid invalid geometry! It cannot be detected automatically.
The positive offset direction is towards the outside of the VNF, the faces that are colored yellow in the "thrown together" view.
The input VNF must not contain duplicate points. By default, vnf_small_offset() calls vnf_merge_points()
to remove duplicate points. Note, however, that this operation can be slow. If you are certain there are no duplicate points you can
set merge=false to disable the automatic point merge and save time. The result of running on a VNF with duplicate points is likely to
be incorrect or invalid.
Arguments:
| By Position | What it does |
|---|---|
vnf |
vnf to offset |
delta |
distance of offset, positive to offset out, negative to offset in |
| By Name | What it does |
|---|---|
merge |
set to false to suppress the automatic invocation of vnf_merge_points(). Default: true |
Example 1: The original sphere is on the left and an offset sphere on the right.
include <BOSL2/std.scad>
vnf = sphere(d=100);
xdistribute(spacing=125){
vnf_polyhedron(vnf);
vnf_polyhedron(vnf_small_offset(vnf,18));
}
Example 2: The polyhedron on the left is enlarged to match the size of the offset polyhedron on the right. Note that the offset does not preserve coplanarity of faces. This is because the vertices all move independently, so nothing constrains faces to remain coplanar.
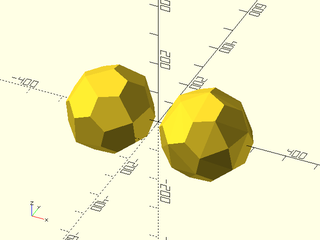
include <BOSL2/std.scad>
include <BOSL2/polyhedra.scad>
vnf = regular_polyhedron_info("vnf","pentagonal icositetrahedron",d=25);
xdistribute(spacing=300){
scale(11)vnf_polyhedron(vnf);
vnf_polyhedron(vnf_small_offset(vnf,125));
}
Function: vnf_sheet()
Synopsis: Extends a VNF into a thin sheet by extruding normal to the VNF [VNF]
Topics: VNF Manipulation
See Also: vnf_small_offset(), vnf_boundary(), vnf_merge_points()
Usage:
- newvnf = vnf_sheet(vnf, thickness, [style=], [merge=]);
Description:
Constructs a thin sheet from a vnf by offsetting the vnf along the normal vectors estimated at each vertex by averaging the normals of the adjacent faces. This is done using {{vnf_small_offset()}. The thickness value must be small enough so that no points cross each other when the offset is computed, because that results in invalid geometry and will give rendering errors. Rendering errors may not manifest until you add other objects to your model. It is your responsibility to avoid invalid geometry!
Once the offset to the original VNF is computed the original and offset VNF are connected by filling in the boundary strip(s) between them
When thickness is positive, the given bezier patch is extended towards its "inside", which is the
side that appears purple in the "thrown together" view. Note that this is the opposite direction
of vnf_small_offset(). Extending toward the inside means that your original VNF remains unchanged
in the output. You can extend the patch in the other direction
using a negative thickness value. When you extend to the outside with a negative thickness, your VNF needs to have all
of its faces reversed to produce a valid polyhedron, so your original VNF is reversed in the output.
The input VNF must not contain duplicate points. By default, vnf_sheet() calls vnf_merge_points()
to remove duplicate points. Note, however, that this operation can be slow. If you are certain there are no duplicate points you can
set merge=false to disable the automatic point merge and save time. The result of running on a VNF with duplicate points is likely to
be incorrect or invalid, or it may result in cryptic errors.
Arguments:
| By Position | What it does |
|---|---|
vnf |
vnf to process |
thickness |
thickness of sheet to produce; can be positive or negative |
| By Name | What it does |
|---|---|
style |
vnf_vertex_array() style to use. Default: "default" |
merge |
if false then do not run vnf_merge_points(). Default: true |
Example 1:
include <BOSL2/std.scad>
pts = [for(x=[30:5:180]) [for(y=[-6:0.5:6]) [7*y,x, sin(x)*y^2]]];
vnf=vnf_vertex_array(pts);
vnf_polyhedron(vnf_sheet(vnf,-10));
Example 2: This example has multiple holes
include <BOSL2/std.scad>
pts = [for(x=[-10:2:10]) [ for(y=[-10:2:10]) [x,1.4*y,(-abs(x)^3+y^3)/250]]];
vnf = vnf_vertex_array(pts);
newface = list_remove(vnf[1], [43,42,63,88,108,109,135,134,129,155,156,164,165]);
newvnf = [vnf[0],newface];
vnf_polyhedron(vnf_sheet(newvnf,2));
Example 3: When applied to a sphere the sheet is constructed inward, so the object appears unchanged, but cutting it in half reveals that we have changed the sphere into a shell.
include <BOSL2/std.scad>
vnf = sphere(d=100, $fn=28);
left_half()
vnf_polyhedron(vnf_sheet(vnf,15));
Section: Debugging Polyhedrons
Module: debug_vnf()
Synopsis: A replacement for vnf_polyhedron() to help with debugging. [VNF]
Topics: VNF Manipulation, Debugging
See Also: vnf_validate()
Usage:
- debug_vnf(vnfs, [faces=], [vertices=], [opacity=], [size=], [convexity=], [filter=]);
Description:
A drop-in module to replace vnf_polyhedron() to help debug vertices and faces.
Draws all the vertices at their 3D position, numbered in blue by their
position in the vertex array. Each face will have its face number drawn
in red, aligned with the center of face. All given faces are drawn with
transparency. All children of this module are drawn with transparency.
Works best with Thrown-Together preview mode, to see reversed faces.
You can set opacity to 0 if you want to supress the display of the polyhedron faces.
The vertex numbers are shown rotated to face you. As you rotate your polyhedron you can rerun the preview to display them oriented for viewing from a different viewpoint.
Arguments:
| By Position | What it does |
|---|---|
vnf |
VNF to display |
| By Name | What it does |
|---|---|
faces |
if true display face numbers. Default: true |
vertices |
if true display vertex numbers. Default: true |
opacity |
Opacity of the polyhedron faces. Default: 0.5 |
convexity |
The max number of walls a ray can pass through the given polygon paths. |
size |
The size of the text used to label the faces and vertices. Default: 1 |
filter |
If given a function literal of signature function(i), will only show labels for vertices and faces that have a vertex index that gets a true result from that function. Default: no filter. |
Example 1:
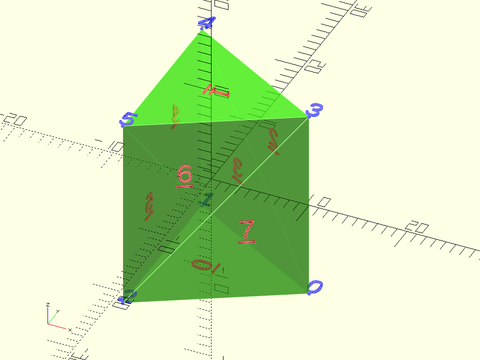
include <BOSL2/std.scad>
verts = [for (z=[-10,10], a=[0:120:359.9]) [10*cos(a),10*sin(a),z]];
faces = [[0,1,2], [5,4,3], [0,3,4], [0,4,1], [1,4,5], [1,5,2], [2,5,3], [2,3,0]];
debug_vnf([verts,faces], size=2);
Module: vnf_validate()
Synopsis: Echos non-manifold VNF errors to the console. [VNF]
Topics: VNF Manipulation, Debugging
See Also: debug_vnf()
Usage:
- vnf_validate(vnf, [size], [show_warns=], [check_isects=], [opacity=], [adjacent=], [label_verts=], [label_faces=], [wireframe=]);
Description:
When called as a module, echoes the non-manifold errors to the console, and color hilites the bad edges and vertices, overlaid on a transparent gray polyhedron of the VNF.
Currently checks for these problems:
| Type | Color | Code | Message |
|---|---|---|---|
| WARNING | Yellow | BIG_FACE | Face has more than 3 vertices, and may confuse CGAL. |
| WARNING | Blue | NULL_FACE | Face has zero area. |
| ERROR | Cyan | NONPLANAR | Face vertices are not coplanar. |
| ERROR | Brown | DUP_FACE | Multiple instances of the same face. |
| ERROR | Orange | MULTCONN | Multiply Connected Geometry. Too many faces attached at Edge. |
| ERROR | Violet | REVERSAL | Faces reverse across edge. |
| ERROR | Red | T_JUNCTION | Vertex is mid-edge on another Face. |
| ERROR | Brown | FACE_ISECT | Faces intersect. |
| ERROR | Magenta | HOLE_EDGE | Edge bounds Hole. |
Still to implement:
- Overlapping coplanar faces.
Arguments:
| By Position | What it does |
|---|---|
vnf |
The VNF to validate. |
size |
The width of the lines and diameter of points used to highlight edges and vertices. Module only. Default: 1 |
| By Name | What it does |
|---|---|
show_warns |
If true show warnings for non-triangular faces. Default: true |
check_isects |
If true, performs slow checks for intersecting faces. Default: false |
opacity |
The opacity level to show the polyhedron itself with. Default: 0.67 |
label_verts |
If true, shows labels at each vertex that show the vertex number. Default: false |
label_faces |
If true, shows labels at the center of each face that show the face number. Default: false |
wireframe |
If true, shows edges more clearly so you can see them in Thrown Together mode. Default: false |
adjacent |
If true, only display faces adjacent to a vertex listed in the errors. Default: false |
Example 1: BIG_FACE Warnings; Faces with More Than 3 Vertices. CGAL often will fail to accept that a face is planar after a rotation, if it has more than 3 vertices.
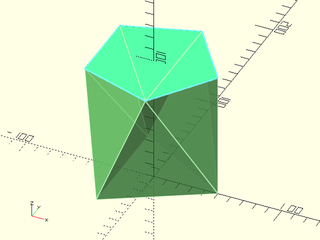
include <BOSL2/std.scad>
vnf = skin([
path3d(regular_ngon(n=3, d=100),0),
path3d(regular_ngon(n=5, d=100),100)
], slices=0, caps=true, method="tangent");
vnf_validate(vnf);
Example 2: NONPLANAR Errors; Face Vertices are Not Coplanar
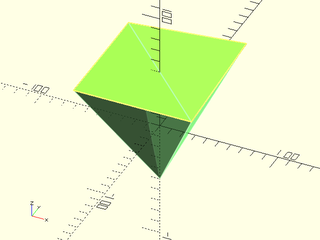
include <BOSL2/std.scad>
a = [ 0, 0,-50];
b = [-50,-50, 50];
c = [-50, 50, 50];
d = [ 50, 50, 60];
e = [ 50,-50, 50];
vnf = vnf_from_polygons([
[a, b, e], [a, c, b], [a, d, c], [a, e, d], [b, c, d, e]
],fast=true);
vnf_validate(vnf);
Example 3: MULTCONN Errors; More Than Two Faces Attached to the Same Edge. This confuses CGAL, and can lead to failed renders.
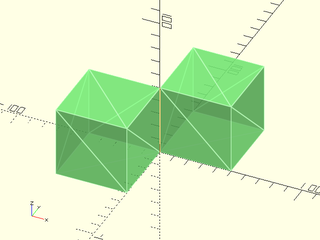
include <BOSL2/std.scad>
vnf = vnf_triangulate(linear_sweep(union(square(50), square(50,anchor=BACK+RIGHT)), height=50));
vnf_validate(vnf);
Example 4: REVERSAL Errors; Faces Reversed Across Edge
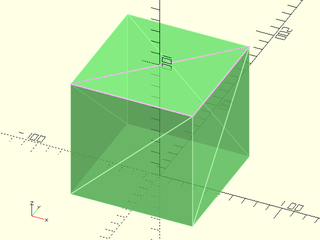
include <BOSL2/std.scad>
vnf1 = skin([
path3d(square(100,center=true),0),
path3d(square(100,center=true),100),
], slices=0, caps=false);
vnf = vnf_join([vnf1, vnf_from_polygons([
[[-50,-50, 0], [ 50, 50, 0], [-50, 50, 0]],
[[-50,-50, 0], [ 50,-50, 0], [ 50, 50, 0]],
[[-50,-50,100], [-50, 50,100], [ 50, 50,100]],
[[-50,-50,100], [ 50,-50,100], [ 50, 50,100]],
])]);
vnf_validate(vnf);
Example 5: T_JUNCTION Errors; Vertex is Mid-Edge on Another Face.
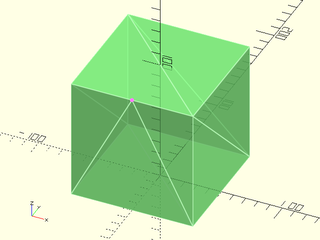
include <BOSL2/std.scad>
vnf = [
[
each path3d(square(100,center=true),0),
each path3d(square(100,center=true),100),
[0,-50,100],
], [
[0,2,1], [0,3,2], [0,8,4], [0,1,8], [1,5,8],
[0,4,3], [4,7,3], [1,2,5], [2,6,5], [3,7,6],
[3,6,2], [4,5,6], [4,6,7],
]
];
vnf_validate(vnf);
Example 6: FACE_ISECT Errors; Faces Intersect
include <BOSL2/std.scad>
vnf = vnf_join([
linear_sweep(square(100,center=true), height=100),
move([75,35,30],p=linear_sweep(square(100,center=true), height=100))
]);
vnf_validate(vnf,size=2,check_isects=true);
Example 7: HOLE_EDGE Errors; Edges Adjacent to Holes.
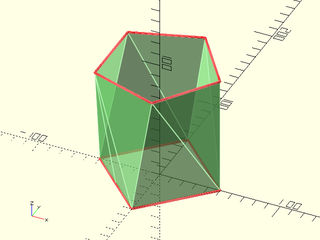
include <BOSL2/std.scad>
vnf = skin([
path3d(regular_ngon(n=4, d=100),0),
path3d(regular_ngon(n=5, d=100),100)
], slices=0, caps=false);
vnf_validate(vnf,size=2);